Difficulties with tgp; taking custom mcmc approach for GPs

Running into some unpredictable and not consistently replicable memory errors in the tgp function calls. Also rather troublesome that return object provides only posterior means for the process mean and covariance matrix.

Generic GP methods

Define some example priors

lpriors <- function(pars){
   d.p <- c(5, 5)
  s2.p <- c(5, 5)  
   
  prior <- unname(
    dgamma(exp(pars[1]), d.p[1], scale = d.p[2]) *
    dgamma(exp(pars[2]), s2.p[1], s2.p[2]) 
  )
  
  log(prior)
}

Define the posterior function for our metropolis sampler

posterior <- function(pars, x, y){
  
  l <- exp(pars[1])
  sigma.n <- exp(pars[2])
  
  cov <- function(X, Y) outer(X, Y, SE, l)
  I <- diag(1, length(x))
  K <- cov(x, x) 
  
  loglik <- - 0.5 * t(y) %*% solve(K + sigma.n^2 * I) %*% y -
    log(det(K + sigma.n^2*I)) -
    length(y) * log(2 * pi) / 2

  loglik + lpriors(pars)
}

I do not think we have good conjugate priors we can use in this situation to accomplish Gibbs sampling. Instead we simply MCMC by the Metropolis-Hastings alogrithm,

require(mcmc)
n <- 1e4
out <- metrop(posterior, log(pars), n, x = obs$x, y = obs$y)
out$accept
[1] 0.1509

Very good, we want an acceptance rate around 20%, if the literature can be trusted on this account. We then plot transformed and untransformed traces.

postdist <- cbind(index=1:n, as.data.frame(exp(out$batch)))
names(postdist) <- c("index", names(pars))
df <- melt(postdist, id="index")
# TRACES
ggplot(df) + geom_line(aes(index, value)) + facet_wrap(~ variable, scale="free", ncol=1)

ggplot(df) + geom_line(aes(index, log(value))) + facet_wrap(~ variable, scale="free", ncol=1)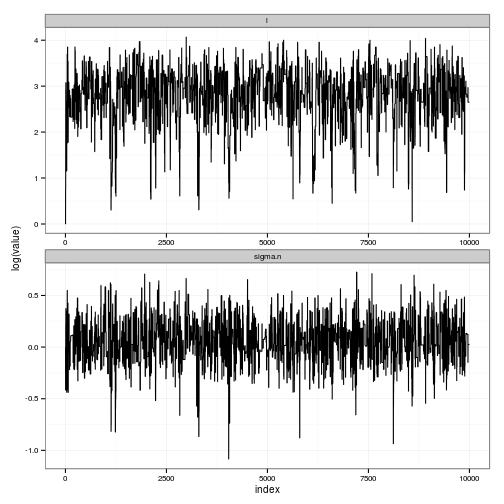

Generate a plot to compare priors and posteriors

d.p <- c(5, 5)
s2.p <- c(5, 5)  
   
s2_prior <- function(x) dgamma(x, s2.p[1], s2.p[2])
d_prior <- function(x) dgamma(x, d.p[1], scale = d.p[2])
prior_fns <- list(l = d_prior, sigma.n = s2_prior)


require(plyr)
prior_curves <- ddply(df, "variable", function(dd){
    grid <- seq(min(dd$value), max(dd$value), length = 100)
    data.frame(value = grid, density = prior_fns[[dd$variable[1]]](grid))
})

# Posteriors (easier to read than histograms)
ggplot(df, aes(value)) + 
  stat_density(geom="path", position="identity", alpha=0.7) +
  geom_line(data=prior_curves, aes(x=value, y=density), col="red") + 
  facet_wrap(~ variable, scale="free", ncol=2)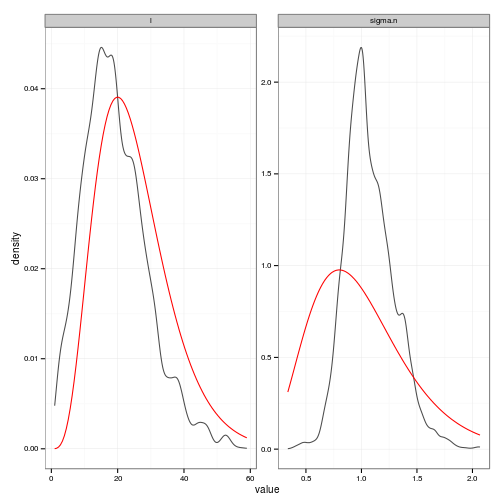
Note that posteriors closely match our priors, as we have only 4 data points in this toy example and our priors are reasonably informative.
Note that posteriors closely match our priors, as we have only 4 data points in this toy example and our priors are reasonably informative.

Steve chat

  1. integrate over posteriors in GP case
  2. Ignore measurement uncertainty for the moment
  3. General status updates, etc.

Marc meeting

  1. Ricker case, but with constraint (e.g. maintain above n%)
  2. Consider Ricker model with external management constraint $ (Y / Y_opt) + (1 - ) Pr( )$
  3. Consider time horizon of learning vs implementing; see diagram

Simone talk

  • General interests: adaptive potential of small pops, demography of small pops, extinction processes in communities, evol life histories & enviroment, ML for species distribution models.

  • Marble trout system under the influence of regular catastrophic floods

Misc