Bayesian Gp Regression By Metropolis Hastings

(Development version for reference; code functions now in R/gp_mcmc.R)

Function definitions

library(mcmc)
#' Basic regression in Gaussian processes  
#' 
#' 
#' @param x Observed x values, (vector or matrix with columns for each dimension of data)
#' @param y Vector of observed y values in the training data
#' @param init_pars the initial guesses for lengthscale l and process noise sigma_n
#' @param n iterations of the metropolis algorithm
#' @details Currently assumes the covariance function.  By default we will use 
#' the squared exponential (also called radial basis or Gaussian, 
#' though it is not this that gives Gaussian process it's name; 
#' any covariance function would do) as the covariance function, 
#' $\operatorname{cov}(X_i, X_j) = \exp\left(-\frac{(X_i - X_j)^2}{2 \ell ^ 2}\right)$
#' @return the MCMC output, as constructed by \link{metrop} from the mcmc package.
#' @export
#' @import mcmc  
gp_mcmc <- function(x, y, init_pars = c(l=1, sigma.n=1), n = 1e4, d.p = c(5,5), s2.p = c(5,5)){

  lpriors <- function(pars){
    prior <- unname(
      dgamma(exp(pars[1]), d.p[1], scale = d.p[2]) *
      dgamma(exp(pars[2]), s2.p[1], s2.p[2]) 
    )
    log(prior)
  }
  posterior <- function(pars, x, y){ 
    l <- exp(pars[1])
    sigma.n <- exp(pars[2])
    
    cov <- function(X, Y) outer(X, Y, SE, l)
    I <- diag(1, length(x))
    K <- cov(x, x) 
    
    loglik <- - 0.5 * t(y) %*% solve(K + sigma.n^2 * I) %*% y -
      log(det(K + sigma.n^2*I)) -
      length(y) * log(2 * pi) / 2
    
    loglik + lpriors(pars)
  }
  
  out <- metrop(posterior, log(init_pars), n, x = obs$x, y = obs$y)  
  out$d.p <- d.p
  out$s2.p <- s2.p
  
  out
}
#' predict the expected values and posterior distributions of the Gaussian Process
#' 
#' @param x_predict the values at which we desire predictions
#' @param covs if TRUE, return covariances instead of variances (set high thinning as this is memory intensive)
#' @import reshape2
#' @export
gp_predict <- function(gp, x_predict, burnin=0, thin=1, covs=FALSE){

  postdist <- cbind(index=1:gp$nbatch, as.data.frame(exp(gp$batch)))
  s <- seq(burnin+1, gp$nbatch, by=thin)
  postdist <- postdist[s,]
  names(postdist) <- c("index", names(gp$initial))
  
  indices <- 1:dim(postdist)[1]
  
  out <- lapply(indices, function(i){
    l <- postdist[i, "l"]
    sigma.n <- postdist[i, "sigma.n"]
    
    cov <- function(X, Y) outer(X, Y, SE, l)
    cov_xx_inv <- solve(cov(obs$x, obs$x) + sigma.n^2 * diag(1, length(obs$x)))
    Ef <- cov(x_predict, obs$x) %*% cov_xx_inv %*% obs$y
    Cf <- cov(x_predict, x_predict) - cov(x_predict, obs$x)  %*% cov_xx_inv %*% cov(obs$x, x_predict)
    list(Ef = Ef, Cf = Cf, Vf = diag(Cf))
  })
  
  Ef_posterior <- sapply(out, `[[`, "Ef")
  Cf_posterior <- sapply(out, `[[`, "Cf")
  Vf_posterior <- sapply(out, `[[`, "Vf")
  
  
  E_Ef <- rowMeans(Ef_posterior)
  E_Cf <- matrix( apply(Cf_posterior, 1, sum) / dim(Cf_posterior)[2], ncol = sqrt(dim(Cf_posterior)[1]) )
  E_Vf <- diag(E_Cf) # same as rowMeans(Vf_posterior)
  
  # list format better for return
  Cf_posterior <- lapply(out, `[[`, "Cf")
  
  list(Ef_posterior = Ef_posterior, 
       Vf_posterior = Vf_posterior,
       Cf_posterior = Cf_posterior,
       E_Ef = E_Ef, E_Cf = E_Cf, E_Vf = E_Vf)
  
}  
library(reshape2)
library(ggplot2)
library(plyr)
#' Summary plots showing the trace and posteriors for the gp_mcmc estimates
#' 
#' @param gp a fit of the gaussian process from gp_mcmc
#' @param burnin length of sequence to discard as a transient
#' @param thin frequency of sub-sampling (make posterior distribution smaller if necessary)
#' @return two ggplot2 objects, one plotting the trace and one 
#' plotting the posteriors in black with priors overlaid in red.  
#' @import reshape2
#' @import ggplot2
#' @import plyr
#' @export
summary_gp_mcmc <- function(gp, burnin=0, thin=1){

  postdist <- cbind(index=1:gp$nbatch, as.data.frame(exp(gp$batch)))
  s <- seq(burnin+1, gp$nbatch, by=thin)
  postdist <- postdist[s,]
  names(postdist) <- c("index", names(gp$initial))
  
  # TRACES
  df <- melt(postdist, id="index")
  traces_plot <- 
    ggplot(df) + geom_line(aes(index, value)) + 
    facet_wrap(~ variable, scale="free", ncol=1)
  
  s2.p <- gp$s2.p
  d.p <- gp$d.p
  s2_prior <- function(x) dgamma(x, s2.p[1], s2.p[2])
  d_prior <- function(x) dgamma(x, d.p[1], scale = d.p[2])
  prior_fns <- list(l = d_prior, sigma.n = s2_prior)
  
  prior_curves <- ddply(df, "variable", function(dd){
    grid <- seq(min(dd$value), max(dd$value), length = 100)
    data.frame(value = grid, density = prior_fns[[dd$variable[1]]](grid))
  })
  
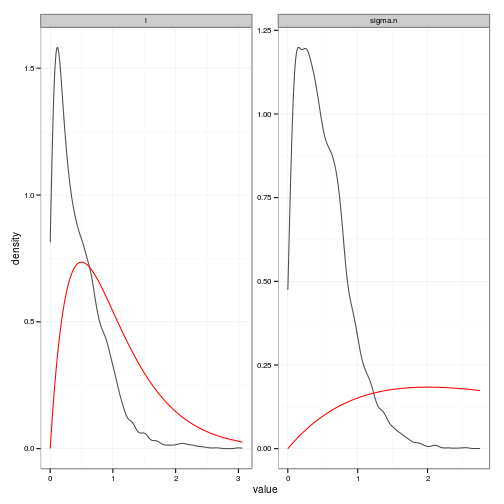
  # Posteriors (easier to read than histograms)
  posteriors_plot <- ggplot(df, aes(value)) + 
    stat_density(geom="path", position="identity", alpha=0.7) +
    geom_line(data=prior_curves, aes(x=value, y=density), col="red") + 
    facet_wrap(~ variable, scale="free", ncol=2)
  
  print(traces_plot)
  print(posteriors_plot)
  
  out <- list(traces_plot = traces_plot, posteriors_plot = posteriors_plot)
  invisible(out)
}

# Helper function: The default covariance function
SE <- function(Xi,Xj, l) exp(-0.5 * (Xi - Xj) ^ 2 / l ^ 2)

Example

x_predict <- seq(-5,5,len=50)
obs <- data.frame(x = c(-4, -3, -1,  0,  2),
                  y = c(-2,  0,  1,  2, -1))
gp <- gp_mcmc(obs$x, obs$y, d.p = c(2,.5), s2.p = c(2,.5))
summary_gp_mcmc(gp)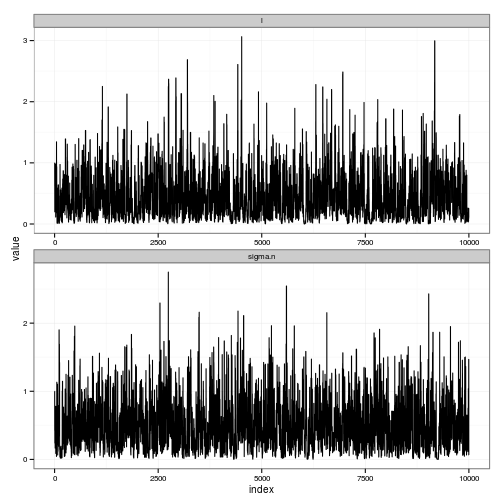

plot of chunk unnamed-chunk-6 plot of chunk unnamed-chunk-6

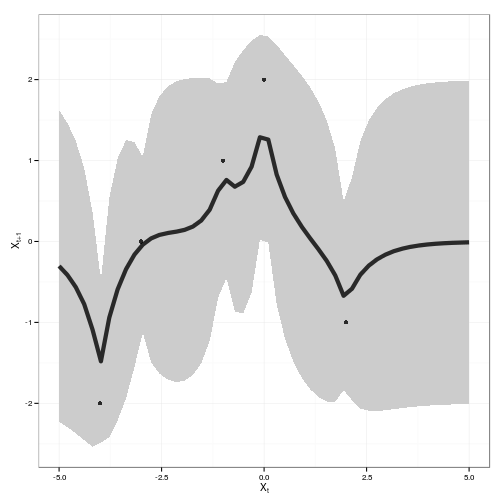
gp_dat <- gp_predict(gp, x_predict)
tgp_dat <- 
    data.frame(  x = x_predict, 
                 y = gp_dat$E_Ef, 
                 ymin = gp_dat$E_Ef - 2 * sqrt(gp_dat$E_Vf), 
                 ymax = gp_dat$E_Ef + 2 * sqrt(gp_dat$E_Vf) )

ggplot(tgp_dat) + geom_ribbon(aes(x,y,ymin=ymin,ymax=ymax), fill="gray80") +
    geom_line(aes(x, y), lwd=2, alpha=0.8) + 
    geom_point(data=obs, aes(x,y), alpha=0.8) + 
    xlab(expression(X[t])) + ylab(expression(X[t+1]))
plot of chunk unnamed-chunk-8
plot of chunk unnamed-chunk-8