Rethinking Beetles Noise

  • Noise in the larval class is damped by 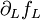\partial_L f_L and grows proportional to its intrinsic variation and the contribution of other classes through their derivatives of fL, that is, 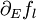\partial_E f_l as well as the sum of its intrinsic rates (essentially whichever is larger). Taking E dynamics to be fast we might reduce to a continous time LPA model:
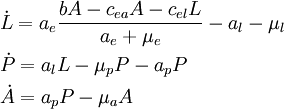
\begin{align} & \dot L = a_e \frac{bA - c_{ea} A - c_{el} L}{a_e + \mu_e} - a_l - \mu_l \\ & \dot P = a_l L - \mu_p P - a_p P \\ & \dot A = a_p P - \mu_a A \end{align}
\begin{align} & \dot L = a_e \frac{bA - c_{ea} A - c_{el} L}{a_e + \mu_e} - a_l - \mu_l \\ & \dot P = a_l L - \mu_p P - a_p P \\ & \dot A = a_p P - \mu_a A \end{align}

and the larval fluctuations are essentially:

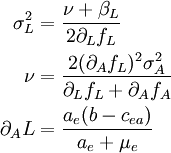
\begin{align} \sigma^2_L &= \frac{\nu + \beta_L}{2 \partial_L f_L} \\ \nu &= \frac{ 2(\partial_A f_L)^2 \sigma_A^2 }{\partial_L f_L + \partial_A f_A} \\ \partial_A L &= \frac{a_e (b - c_{ea} ) }{a_e + \mu_e} \end{align}
\begin{align} \sigma^2_L &= \frac{\nu + \beta_L}{2 \partial_L f_L} \\ \nu &= \frac{ 2(\partial_A f_L)^2 \sigma_A^2 }{\partial_L f_L + \partial_A f_A} \\ \partial_A L &= \frac{a_e (b - c_{ea} ) }{a_e + \mu_e} \end{align}

where βi is the intrinsic noise of the age class. Hence a class i which propagates large noise to another class j has a large 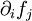\partial_i f_j. If this term is a linear transition λXi, then the same term appears in fi and hence damps the noise 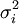\sigma_i^2 and cancels out. Hence noise must propagate into a class through nonlinear transition rates OR through an asymmetry in the transition (i.e. the c_1, c_2 large noise example in the generalized crowley).


Compare to noise in Eggs:

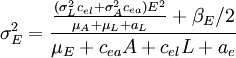
\sigma^2_E = \frac{ \frac{ (\sigma_L^2 c_{el} +\sigma_A^2 c_{ea} )E^2 }{\mu_A + \mu_L + a_L}+ \beta_E/2}{\mu_E + c_{ea} A + c_{el} L + a_e}
\sigma^2_E = \frac{ \frac{ (\sigma_L^2 c_{el} +\sigma_A^2 c_{ea} )E^2 }{\mu_A + \mu_L + a_L}+ \beta_E/2}{\mu_E + c_{ea} A + c_{el} L + a_e}


Adding age delay to beetle dynamics ———————————–

Current formulation has used exponential waiting times between stages. By subdividing the classes (increasing the system dimension size) and creating single jump within-state transitions, these become gamma-distributed waiting times. Adding ten steps to each phase and a little parameter fiddling introduces sustained oscillations. (Version-stable code).


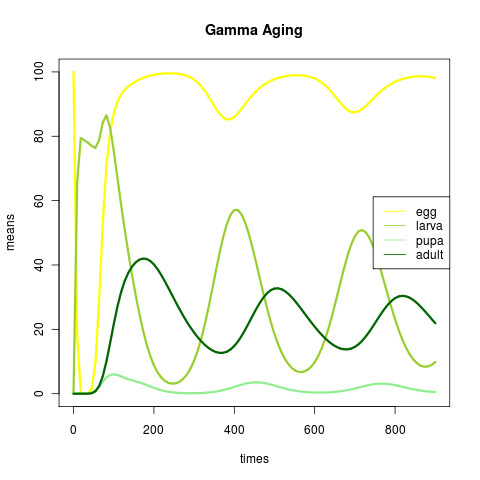
image


beetle_pars <- c(b=5, ue= 0, ul = 0.001, up = 0.00001, ua = 0.01, ae = 1.3, al = .1, ap = 1.5, cle = .2, cap = .1, cae = 5, V=100)

Xo[1] = 100

  • Implementation still needs trouble-shooting, variance dynamics don’t seem to be being computed correctly. done
  • Adult class doesn’t need multiple stages. done
  • Code should allow for a general k classes rather than a fixed 10 classes. done

and now we have noise in oscillatory, gamma-waiting model:

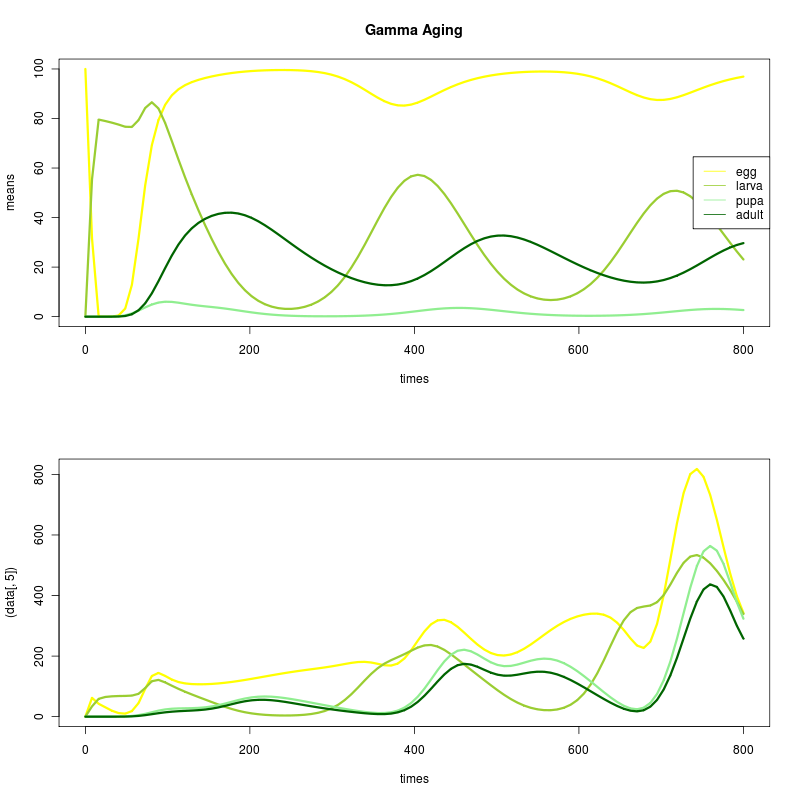
image
image


Misc / Code notes —————–

  • R-evolution parallelizes the variance dynamics calculation (perhaps the matrix multiplication step?) and is probably responsible for the openmp parallelization working.

  • article on cloud computing vs grid. reminds me to include questions on cloud computing in the CSGF survey.

  • Should also take a closer read of the recent: Kendall BE, Wittmann ME. A stochastic model for annual reproductive success. The American naturalist. 2010;175(4):461-8. Available at: https://www.ncbi.nlm.nih.gov/pubmed/20163244.