Meeting

  • Basically I want to apply central limit theorem for stationary processes (accounts for covariances), assuming mean zero
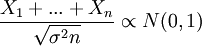
\frac{X_1 + … + X_n}{\sqrt{\sigma^2 n}} \propto N(0,1)
\frac{X_1 + … + X_n}{\sqrt{\sigma^2 n}} \propto N(0,1)

where

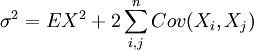
\sigma^2 = E X^2 + 2 \sum_{i,j}^n Cov(X_i, X_j)
\sigma^2 = E X^2 + 2 \sum_{i,j}^n Cov(X_i, X_j)
  • Discussion of Freidlin-Wentzell theory in connection to Arrhenius law and the well-defined stochastic tipping point which occurs before the branch point.
  • Kurtz results don’t really help in the case of ergodicity, can make statements about the (even non-stationary) ensemble limit.