Bodega Phylogenetics Workshop Day 1

Lecture notes for the phyolgenetics workshop. These are taken in real time, so may contain errors. I’ll see if I keep this up throughout the course. See course website.

Huelsenbeck

9a-11a

  • Parameters θ
  • Observation X
  • p(X | θ) is known as the likelihood. Adjust parameter to maximize likelihood.
  • Coin toss example

θ = prob of heads on a single toss of a coin, X is # of heads observed on n tosses. Choose a model: binomial:

p(x|\theta) = {n \choose{x}} \theta^x ( 1-\theta)^{n-x}
p(x|\theta) = {n \choose{x}} \theta^x ( 1-\theta)^{n-x}
  • Maximize likelihood, find \hat \theta = \frac{x}{n}
  • Bayesian
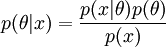
p(\theta | x) = \frac{p(x|\theta)p(\theta)}{p(x)}
p(\theta | x) = \frac{p(x|\theta)p(\theta)}{p(x)}

likelihood times prior over marginal equals the posterior. The prior is the source of controversy, though mathematically required if you want a posterior probability.

The marginal can be hard to solve. 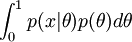\int_0^1 p(x|\theta) p(\theta) d\theta

So Bayesians solved trivial problems or just estimated moments (mean, etc), until along came MCMC and they could do these integrals…

Phylogenetic Model

  • Parameters: Tree. (comments on notation). Life is more simple than you think: all phylogenetic models are continuous time Markov models
  • “Observations:” could be:
    • Alignment (note that it’s not actually observed, it’s an inference from the chronogram from the sequencer! we’ll ignore that.)
    • Character matrix

Calculate the probability of alignment given a tree?

  • (Lecture moves to slides, will probably ve available on Bodega Wiki?)

  • Summing over all possible combinations literally is crazy. Felsenstein Pruning algorithm (sum-product algorithm from graphical models) makes this much faster (many of those trees are related).

  • “This is the exponential distribution, it is the only distribution you’ll see/need in this course”

moments later…

  • “This is the gamma distribution, it is the only distribution you’ll need”
  • “Oh, and this is the Poisson distribution.”


Dice activity: Exact simulation of finite-state continuous time Markov process

  • Interesting hands-on activity to demonstrate Gillespie algorithm simulation.

Codon models.

  • (Note, this wiki entry should be expanded).
  • Sequence model, sparse matrices with arbitrary correlations. Approximate pruning via MCMC.

  • Rate variation across sites.

    • Approximate the gamma by likelihood catagories, using the mean of a catagory.
li = ∑ p(xi | x) / k
k
    • Heterotachy – different models on different parts of the tree.
    • Nielsen & Yang 1998


### Jeremy Brown, Mr. Bayes

Using Mr. Bayes

  • Can’t calculate the marginal probability. Luckily, in ratio that normalizing constant cancels out: So we can find the ratio of posterior probabilities. This is where MCMC comes in.

See the slides

Rannala, Divergence Times

  • Molecular clock and fossil dating
  • branch lengths as estimates
  • Bayesian approaches to contain this uncertainty, given sequences times and fossil calibrations:
f(\theta, t, u | X) = \frac{f(X|t,u,\theta)f(u|\theta) f(t| \theta) f(\theta) }{f(X)}
f(\theta, t, u | X) = \frac{f(X|t,u,\theta)f(u|\theta) f(t| \theta) f(\theta) }{f(X)}

substitution rate (clock) u, branch length v, age t.

Prior for the divergence times. Priors from fossils. Dangers of hard bounds (will confidently predict the wrong answer).

When do you have enough DNA sequence that your divergence estimate becomes limited only by fossil age uncertainty? Regress width of posterior distribution for divergence times against the mean. Once that regression is sufficiently tight, more DNA data won’t help.

  • Irregular Molecular clocks


### Tom Near, Rocks for Gel Jocks

(a.k.a) BEAST tutorial

slides


Ideas/Topics ————

  • Reaching the developers
    • Help lists.
    • uservoice.
    • stackoverflow for phylogenetics?
  • Managing the literature: Mendeley
  • Poll faculty for useful software,tools or tricks. Attempt a talk: 5 minutes, 5 tools to change your life.
    • Mendeley: an itunes for your pdfs, pandora for the literature.


### Thoughts/things to investigate or share

  • When, if ever, can you actually fit a model with trending rate changes over time. i.e. can we really detect accelerating BM in character evolution?
  • Common intuitive mechanisms that generate the familiar distributions. Exponential, Poisson, Gamma, Normal, Log Normal, Binomial, Uniform, Dirchlet.