If you do know the model and are simply uncertain about the parameters, you can often do all right (e.g. better than maximum likelihood approach) by doing the SDP over the Bayesian posterior distribution of the estimated model. Not surprisingly, if you don’t have the correct model, this can fail pretty dramatically (in particular in very nonlinear models, e.g. tipping point models I have been looking at). Model choice and model averaging approaches aren’t much help here, because often the structurally correct model doesn’t fit the observed data any better – since the problems occur due to model inaccuracies where we don’t have data; e.g. near the tipping point.
The surprising thing (to me anyway) is that using an appropriate nonparametric Bayesian process (e.g. Gaussian processes) to approximate the dynamics in place of a parametric model, I can often do just as well as having the correct model structure! I believe this works because I get a better description of the uncertainty in regions where I don’t have data.
I’m trying to write this work up now. It’s a bit of a nuisance because you always have to convince yourself that the differences in performance aren’t just due to MCMC convergence issues, so there’s a wealth of nuisance parameters to worry about.
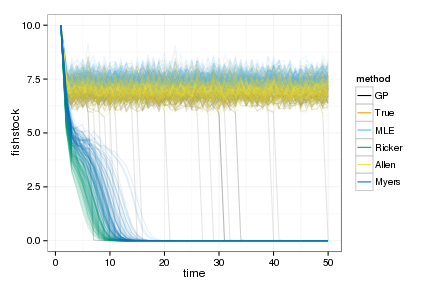
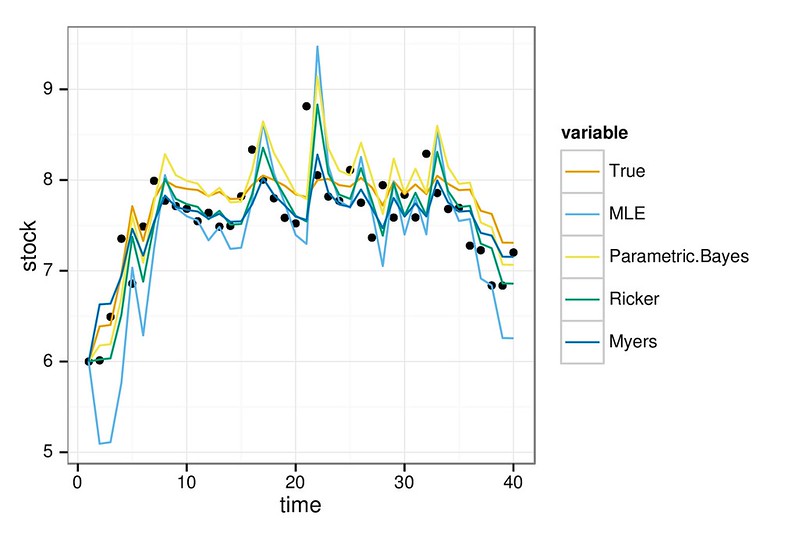
You can see the basic idea here. All models can fit the data reasonably well…
But the wrong parametric models cause the SDP to crash the stock, while the GP or the correct structural estimate perform about as well as you would using the true simulation parameters (e.g. GP, True, and correct structured “Allen” model all like on top of each other):