Warning Signals

Alternate models

  • Writing down the change-point model correctly now, starting with the simulation. Done. Implemented in sde_likelihood.R

  • Implementing Neyman-Pearson comparisons for all three models.

Linearizing directly from the saddle node model

Dynamics:

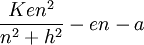
\frac{K e n^2}{n^2 + h^2} - e n - a
\frac{K e n^2}{n^2 + h^2} - e n - a

Slope (alpha) at equilibrium comes from the derivative:

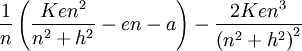
\frac{1}{n} \left( \frac{K e n^2}{n^2 + h^2} - e n - a \right) -\frac{2 K e n^3}{\left( n^2 + h^2 \right)^2}
\frac{1}{n} \left( \frac{K e n^2}{n^2 + h^2} - e n - a \right) -\frac{2 K e n^3}{\left( n^2 + h^2 \right)^2}
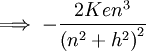
\implies -\frac{2 K e n^3}{\left( n^2 + h^2 \right)^2}
\implies -\frac{2 K e n^3}{\left( n^2 + h^2 \right)^2}

is the slope evaluated at n equal to equilbrium (which is the root of some messy cubic).