Graham & Peter Meeting

Fantastic meeting with Graham and Peter today, covered a lot of ground.

MNV

I briefly sketched the multivariate normal solution for joint probability across the tree under the regimes model. The original regimes approach did not take advantage of the fact that the solution to the joint probability across the tree is multivariate normal given the painting. This allows the calculation to be partitioned as outlined in Saturday’s entry:

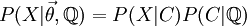
P(X | \vec \theta, \mathbb{Q} ) = P(X | C) P(C | \mathbb{Q} )
P(X | \vec \theta, \mathbb{Q} ) = P(X | C) P(C | \mathbb{Q} )


#### Importance Sampling

  • The method I had outlined by reusing the tree library and weighting by the probability that the Q matrix generated that tree goes by the name Importance Sampling, though it ought to have been re-weighted by the probability it was produced from the original Q matrix used to generate it (Q’), and then averaged. (In my examples (github) I generate from the same distribution as a weight from and these agree). A brief summary excerpted from Wikipedia:


\begin{align} p_t & {} = {E} [1(X \ge t)] \\ & {} = \int 1(x \ge t) \frac{f(x)}{f_*(x)} f_*(x) \,dx \\ & {} = {E_*} [1(X \ge t) W(X)] \end{align}

where

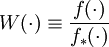
W(\cdot) \equiv \frac{f(\cdot)}{f_*(\cdot)}
W(\cdot) \equiv \frac{f(\cdot)}{f_*(\cdot)}

is a likelihood ratio and is referred to as the weighting function. The last equality in the above equation motivates the estimator

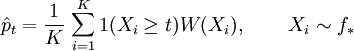
\hat p_t = \frac{1}{K}\,\sum_{i=1}^K 1(X_i \ge t) W(X_i),\,\quad \quad X_i \sim f_*
\hat p_t = \frac{1}{K}\,\sum_{i=1}^K 1(X_i \ge t) W(X_i),\,\quad \quad X_i \sim f_*

This is the importance sampling estimator of 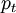p_t\, and is unbiased. That is, the estimation procedure is to generate i.i.d. samples from 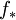f_*\, and for each sample which exceeds 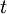t\,, the estimate is incremented by the weight 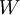W\, evaluated at the sample value. The results are averaged over 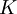K\, trials.


- Unfortunately having to know the 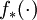f_*(\cdot) term means that I cannot produce the painting library arbitrarily, but will be stuck finding the right painting only with the probability that I can simulate it from the prior.

MCMC

Partitioning the problem

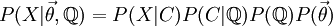
P(X | \vec \theta, \mathbb{Q} ) = P(X | C) P(C | \mathbb{Q} ) P( \mathbb{Q} ) P( \vec \theta)
P(X | \vec \theta, \mathbb{Q} ) = P(X | C) P(C | \mathbb{Q} ) P( \mathbb{Q} ) P( \vec \theta)

and proposing paintings directly, we can MCMC over the space of possible paintings C, OU parameters 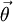\vec \theta and transition matrices 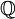\mathbb{Q}. Still, as this problem is hard in the discrete case over 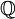\mathbb{Q} (BayesTraits), optimizing the MCMC will still be interesting…

  • Discussion of Hastings ratio
  • Discussion of reversible jump

Wainwright Lab Meeting, 4-6pm

Presented three potential questions to focus on for the Evolution talk:

  1. Defining clusters from raw data, with example in Labrids
  2. Inferring paintings and transition rates directly from data via MCMC
  3. Risks in AIC-based model choice

The group clearly indicated that I should focus on the third, AIC topic, as it is the furthest along and the most immediate impact to the audience. Surprising to me as it is also the least biologically driven. Back to the drawing board now to figure out how to tell this story clearly and succinctly.