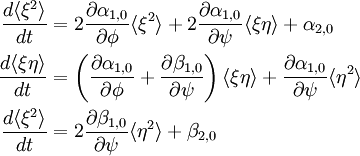Goals
- van Kampen expansion of LPA model, maximize noise in L while keeping A robust?
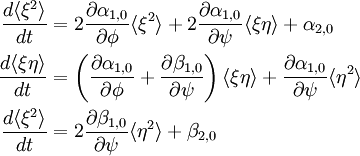\begin{align} \frac{d \langle \xi^2 \rangle}{d t} &= 2 \frac{\partial \alpha_{1,0}}{\partial \phi} \langle \xi^2 \rangle + 2 \frac{\partial \alpha_{1,0} }{\partial \psi} \langle \xi \eta \rangle + \alpha_{2,0} \\ \frac{d \langle \xi \eta \rangle}{d t} &= \left( \frac{\partial \alpha_{1,0}}{\partial \phi} + \frac{\partial \beta_{1,0} }{\partial \psi} \right)\langle \xi \eta \rangle+ \frac{\partial \alpha_{1,0} }{\partial \psi} \langle \eta^2 \rangle \\ \frac{d \langle \xi^2 \rangle}{d t} &= 2 \frac{\partial \beta_{1,0}}{\partial \psi} \langle \eta^2 \rangle + \beta_{2,0} \end{align}
- Indiv. heterogeneity issue: dividing larval class into a smaller, highly-cannibal and remainder of more weakly cannibalistic.
- Pulse dynamics – interspike interval, magnitude?
Potential Data
- 1995 Dennis et al. – 5 replicate populations (2-cycle dataset), 5 age-cycles.
- eight-year chaotic time series
- Strawbridge daily samples (single replicate), occasional disease in lines though.
Literature
- Caswell 2009 Sensitivity of density dependent dynamics
- Kendall (yet unpublished)
- Vindenes 2008 Individual heterogeneity & demographic stochasticity.
- Ludwig 1996 Failure of diffusion approximation in small populations.
Next Steps
- Analytic description of large demographic noise systems
- Comparisons to beetle datasets
- Paper Outline. Skype meeting May 28th.