Alan Meeting

  • Goals next week: Bob & Brian beetle data: what an analysis would be with complete stochastic description.
  • Compare models with different

Full model: Parameter list from current code:

 /* Biological Parameters.  eggs and pupa can get canibalized */
    double b = 5;                                                   /* Birth rate (per day) */
    double u_egg = 0, u_larva = 0.001, u_pupa = 0, u_adult = 0.003; /* Mortality rate (per day) */
    double a_egg = 3.8, a_larva = 3.8+16.4, a_pupa = 3.8+16.4+5.0;    /* age at which each stage matures, in days */
    double cannibal_larva_eggs = 0.01, cannibal_adults_pupa = 0.004, cannibal_adults_eggs = 0.01; /* cannibalism of x on y, per day */
    double a_larva_asym = 3.8+8.0;                                  /* age after which larval size asymptotes */
  • Add individual heterogeneity in egg and larva maturation age and in cannibalism of larva on eggs.

Outline / manuscript draft

Likelihood inference for time series

  • All based on step-ahead predictions, from Markov property. Compare to deterministic skeleton’s minimization of sum of squares on step-ahead predictions (i.e. assumes normal deviates).


See the monographs:

  • Iacus, S. M. (2008). Simulation and Inference for Stochastic Differential Equations With R Examples. New York: Springer.
  • Prakasa Rao, B.L.S. (1999) Statistical Inferences for Diffusion Type Processes, Oxford University Press, New York.

Exploring existing implementations of likelihood methods on SDEs through the R sde package accompanying the Iacus text.

  • Many nice methods for SDEs, general case is harder.

Conditions

  • Large sample scheme Time interval gets longer with n, while Δ is fixed time-step. Requires the additional assumptions of stationarity and/or ergodicity
  • High-frequency scheme: Δ shrinks as n increases, fixed window, need not assume ergodic.
  • Rapidly increasing design: hybrid combination with prescribed rate of mesh increase k

Underlying model

dXt = b(Xt,θ)dt + σ(Xt,θ)*d**W*t

Exact Likelihood conditions

  • Linear growth assumption:
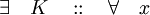
\exists \quad K \quad :: \quad \forall \quad x
\exists \quad K \quad :: \quad \forall \quad x
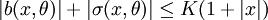
|b(x,\theta)| + |\sigma(x,\theta)| \leq K(1+|x|)
|b(x,\theta)| + |\sigma(x,\theta)| \leq K(1+|x|)
  • Global Lipshitz assumption:

b(x,θ) − b(y,θ) | + σ(x,θ) − σ(y,θ) < K | x − y |

  • Positive diffusion coefficient

  • Bounded moments

  • Smooth coefficients (will use up to 3 times differentiable)

Convergence of diffusion part estimator usually 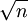\sqrt n, with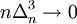 n \Delta_n^3 \to 0

Numerical methods

  • Exact likelihood inference (conditional density of process must be known)
  • Euler approximation: discretization can assume linearity over small Δt
  • Elerian method (Milstein scheme)
  • Kessler (higher order Ito/Taylor expansion)
  • Simulated likelihood (approximate cdf with subdivisions in timestep over which Euler is accurate).
  • Hermite polynomial expansion of likelihood.


#### Steps

  1. Evaluate the conditional density function
  2. Evaluate the likelihood function (will be used as single step predictor)
  3. maximum likelihood estimation

Code updates

  • Swapped out my original linked list library for a more intelligent one. Not sure why pointer pointers are so useful but valgrind is happy.
  • beetle simulator now creates step-ahead realizations.
  • Considerations: replicates in C or R? would be better if R preserved the openmp code, but can always use parallel R to loop over timesteps and benefit from compiled speed on replicates.
  • Kernel density estimation for assigning probabilities? Probably reserve at R level at the moment.


Misc Reading & Notes ——————–