Phylogenetic Tree formats

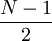  • Consider a tree with N nodes. has \frac{N+1}{2} tips and \frac{N-1}{2} internal nodes.

ape Format: class “phylo”

  • Elements of the data structure:
  • phy$edge – Topology. 2 by N-1 matrix. First column has internal nodes only, each node appearing twice. Internal nodes range from 1+(N+1)/2 to N-1, while the tip numbers go from 1 to (N+1)/2. Each node appears once in the second column, and is a child of the node identified in the first column.

The order of the rows in the matrix doesn’t matter.

  • phy\(edge.length -- the N-1 length numeric. Lengths of the edges in the same order as phy\)edge. Optional for plotting.
  • phy$tip.label – \frac{N+1}{2} length character vector. The index values correspond to the
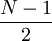
  • phy$Nnode – Number of internal nodes, equals \frac{N-1}{2}

These are the essential components of a phylo object. Optional parameter includes a list of names for internal nodes:

  • phy <- makeNodeLabel(phy) adds phy$node.label
  • phy$node.label

Ape format is very picky. Any tree topology is completely specified by listing the ancestor for each node. If the nodes are identified as 1:n, then the topology is an ordered vector of length n. This is the representation used by ouch. The node numbers can be arbitrary identifiers. Ape chooses a more restrictive representation. Nodes are assigned numbers such that the numbers 1 to (n+1)/2 are assigned exclusively to tips, and those after are assigned exclusively to internal nodes. Topology is specified by listing the ancestor of each node. The identity is stored in edge[,2] and the ancestor in edge[,1]. However, it appears that the root node cannot be assigned as n. Whichever is the ancestor will be missing from the node list on the right (edge[,2]), as it has no corresponding ancestor on the left. It seems the (n+1)/2 + 1 does best assigned to the root. Ouch2ape conversion could easily preserve the node-numbering used in the ape representation, but for some reason the function chooses to renumber them anyway. Reversing is harder, as not all applicable codings of a tree in the ouch representation meet the additional constraints of the ape tree.


#### ouch Format: class “ouchtree”

  • Topology specified in tree@ancestors
  • each node lists its ancestor
  • fitted models have class “hansentree” or “browntree” and contain parameter fitting details.