Comparing to Analytic Dynamics

Goal for today: implement analytic calculations for warning signals.

  • 10am-12pm

Abstraction/functionalizing code.

  • 4pm-7pm

Implement GSL ode solvers for linear noise approximation:

Recall our dynamics are 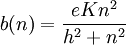b(n) = \frac{e K n^2}{h^2+n^2}

d(n) = *e**n* + a

and defining the jump moments (van Kampen) α1(n) = b(n) − d(n)

α2(n) = b(n) + d(n)


recall that we have a linear Fokker-Planck equation whose solution is Gaussian and specified by the first two moments: 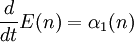\frac{d}{dt} E(n) = \alpha_1(n)

\frac{d}{dt} \sigma^2_n = 2 \sigma_2(n) \frac{d}{dn} \alpha_1(n) + \alpha_2(n)
\frac{d}{dt} \sigma^2_n = 2 \sigma_2(n) \frac{d}{dn} \alpha_1(n) + \alpha_2(n)
  • These are implemented in code using GSL ode library.
  • The variance calculation seems not to agree with the simulated results, though no obvious bug. Perhaps I’ve been too cavalier about the scaling above?
  • Will try implementing simpler functions I’ve tested before to confirm.
  • Need to repeat this analysis for the multivariate case where parameter a changes dynamically at specified rate.
  • Will also consider making a change according to stochastic rules, adding environmental variability.


### svn log

r22 | cboettig | 2010-02-23 23:45:12 -0800 (Tue, 23 Feb 2010) | 1 line

Implemented ode functions solving the linear noise approximation equations. Mean agrees well, variance calculation seems off.

r21 | cboettig | 2010-02-23 11:39:25 -0800 (Tue, 23 Feb 2010) | 2 lines

gillespie.h and gillespie.c abstraction completed. Documentation should still explain how to create the necessary functions to run a gillespie simulation, but is otherwise complete.

r20 | cboettig | 2010-02-23 10:30:03 -0800 (Tue, 23 Feb 2010) | 2 lines

Functionalizing code into seperate files. The main gillespie code has been broken off into its own file, gillespie.c along with its own header. To keep the function calls agnostic to the details of the parameters structure, all the gillespie functions my_pars is passed as a void pointer and promoted to a pars pointer inside the function defs.