Comparison of Nonparametric Bayesian Gaussian Process estimates to standard the Parametric Bayesian approach
Plotting and knitr options, (can generally be ignored)
require(modeest)
posterior.mode <- function(x) {
mlv(x, method="shorth")$M
}Model and parameters
Uses the model derived in citet("10.1080/10236190412331335373"), of a Ricker-like growth curve with an allee effect, defined in the pdgControl package,
f <- RickerAllee
p <- c(2, 8, 5)
K <- 10 # approx, a li'l' less
allee <- 5 # approx, a li'l' lessVarious parameters defining noise dynamics, grid, and policy costs.
sigma_g <- 0.05
sigma_m <- 0.0
z_g <- function() rlnorm(1, 0, sigma_g)
z_m <- function() 1+(2*runif(1, 0, 1)-1) * sigma_m
x_grid <- seq(0, 1.5 * K, length=50)
h_grid <- x_grid
profit <- function(x,h) pmin(x, h)
delta <- 0.01
OptTime <- 50 # stationarity with unstable models is tricky thing
reward <- 0
xT <- 0
Xo <- allee+.5# observations start from
x0 <- K # simulation under policy starts from
Tobs <- 40Sample Data
set.seed(1234)
#harvest <- sort(rep(seq(0, .5, length=7), 5))
x <- numeric(Tobs)
x[1] <- Xo
nz <- 1
for(t in 1:(Tobs-1))
x[t+1] = z_g() * f(x[t], h=0, p=p)
obs <- data.frame(x = c(rep(0,nz),
pmax(rep(0,Tobs-1), x[1:(Tobs-1)])),
y = c(rep(0,nz),
x[2:Tobs]))
raw_plot <- ggplot(data.frame(time = 1:Tobs, x=x), aes(time,x)) + geom_line()
raw_plot
Maximum Likelihood
set.seed(12345)
estf <- function(p){
mu <- f(obs$x,0,p)
-sum(dlnorm(obs$y, log(mu), p[4]), log=TRUE)
}
par <- c(p[1]*rlnorm(1,0,.4),
p[2]*rlnorm(1,0,.3),
p[3]*rlnorm(1,0, .3),
sigma_g * rlnorm(1,0,.3))
o <- optim(par, estf, method="L", lower=c(1e-5,1e-5,1e-5,1e-5))
f_alt <- f
p_alt <- c(as.numeric(o$par[1]), as.numeric(o$par[2]), as.numeric(o$par[3]))
sigma_g_alt <- as.numeric(o$par[4])
est <- list(f = f_alt, p = p_alt, sigma_g = sigma_g_alt, mloglik=o$value)Mean predictions
true_means <- sapply(x_grid, f, 0, p)
est_means <- sapply(x_grid, est$f, 0, est$p)Non-parametric Bayes
#inv gamma has mean b / (a - 1) (assuming a>1) and variance b ^ 2 / ((a - 2) * (a - 1) ^ 2) (assuming a>2)
s2.p <- c(5,5)
d.p = c(10, 1/0.1)Estimate the Gaussian Process (nonparametric Bayesian fit)
gp <- gp_mcmc(obs$x, y=obs$y, n=1e5, s2.p = s2.p, d.p = d.p)
gp_dat <- gp_predict(gp, x_grid, burnin=1e4, thin=300)Show traces and posteriors against priors
plots <- summary_gp_mcmc(gp, burnin=1e4, thin=300)
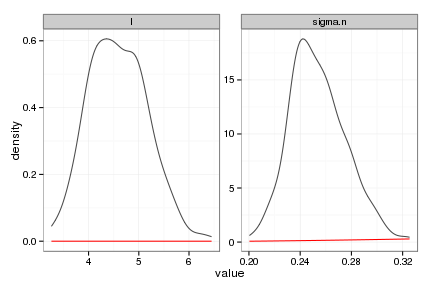
# Summarize the GP model
tgp_dat <-
data.frame( x = x_grid,
y = gp_dat$E_Ef,
ymin = gp_dat$E_Ef - 2 * sqrt(gp_dat$E_Vf),
ymax = gp_dat$E_Ef + 2 * sqrt(gp_dat$E_Vf) )Parametric Bayesian Models
We use the JAGS Gibbs sampler, a recent open source BUGS implementation with an R interface that works on most platforms. We initialize the usual MCMC parameters; see ?jags for details.
All parametric Bayesian estimates use the following basic parameters for the JAGS MCMC:
y <- x
N <- length(x);
jags.data <- list("N","y")
n.chains <- 6
n.iter <- 1e6
n.burnin <- floor(10000)
n.thin <- max(1, floor(n.chains * (n.iter - n.burnin)/1000))
n.update <- 10We will use the same priors for process and observation noise in each model,
stdQ_prior_p <- c(1e-6, 100)
stdR_prior_p <- c(1e-6, .1)
stdQ_prior <- function(x) dunif(x, stdQ_prior_p[1], stdQ_prior_p[2])
stdR_prior <- function(x) dunif(x, stdR_prior_p[1], stdR_prior_p[2])Parametric Bayes of correct (Allen) model
We initiate the MCMC chain (init_p) using the true values of the parameters p from the simulation. While impossible in real data, this gives the parametric Bayesian approach the best chance at succeeding. y is the timeseries (recall obs has the \(x_t\), \(x_{t+1}\) pairs)
The actual model is defined in a model.file that contains an R function that is automatically translated into BUGS code by R2WinBUGS. The file defines the priors and the model. We write the file from R as follows:
K_prior_p <- c(0.01, 40.0)
logr0_prior_p <- c(-6.0, 6.0)
logtheta_prior_p <- c(-6.0, 6.0)
bugs.model <-
paste(sprintf(
"model{
K ~ dunif(%s, %s)
logr0 ~ dunif(%s, %s)
logtheta ~ dunif(%s, %s)
stdQ ~ dunif(%s, %s)",
K_prior_p[1], K_prior_p[2],
logr0_prior_p[1], logr0_prior_p[2],
logtheta_prior_p[1], logtheta_prior_p[2],
stdQ_prior_p[1], stdQ_prior_p[2]),
"
iQ <- 1 / (stdQ * stdQ);
r0 <- exp(logr0)
theta <- exp(logtheta)
y[1] ~ dunif(0, 10)
for(t in 1:(N-1)){
mu[t] <- y[t] * exp(r0 * (1 - y[t]/K)* (y[t] - theta) / K )
y[t+1] ~ dnorm(mu[t], iQ)
}
}")
writeLines(bugs.model, "allen_process.bugs")Write the priors into a list for later reference
K_prior <- function(x) dunif(x, K_prior_p[1], K_prior_p[2])
logr0_prior <- function(x) dunif(x, logr0_prior_p[1], logr0_prior_p[2])
logtheta_prior <- function(x) dunif(x, logtheta_prior_p[1], logtheta_prior_p[2])
par_priors <- list(K = K_prior, deviance = function(x) 0 * x,
logr0 = logr0_prior, logtheta = logtheta_prior,
stdQ = stdQ_prior)We define which parameters to keep track of, and set the initial values of parameters in the transformed space used by the MCMC. We use logarithms to maintain strictly positive values of parameters where appropriate.
jags.params=c("K","logr0","logtheta","stdQ") # be sensible about the order here
jags.inits <- function(){
list("K"= 8 * rlnorm(1,0, 0.1),
"logr0"=log(2 * rlnorm(1,0, 0.1) ),
"logtheta"=log( 5 * rlnorm(1,0, 0.1) ),
"stdQ"= abs( 0.1 * rlnorm(1,0, 0.1)),
.RNG.name="base::Wichmann-Hill", .RNG.seed=123)
}
set.seed(1234)
# parallel refuses to take variables as arguments (e.g. n.iter = 1e5 works, but n.iter = n doesn't)
allen_jags <- do.call(jags.parallel, list(data=jags.data, inits=jags.inits,
jags.params, n.chains=n.chains,
n.iter=n.iter, n.thin=n.thin,
n.burnin=n.burnin,
model.file="allen_process.bugs"))
# Run again iteratively if we haven't met the Gelman-Rubin convergence criterion
recompile(allen_jags) # required for parallel
allen_jags <- do.call(autojags, list(object=allen_jags, n.update=n.update,
n.iter=n.iter, n.thin = n.thin))Convergence diagnostics for Allen model
R notes: this strips classes from the mcmc.list object (so that we have list of matrices; objects that reshape2::melt can handle intelligently), and then combines chains into one array. In this array each parameter is given its value at each sample from the posterior (index) for each chain.
tmp <- lapply(as.mcmc(allen_jags), as.matrix) # strip classes the hard way...
allen_posteriors <- melt(tmp, id = colnames(tmp[[1]]))
names(allen_posteriors) = c("index", "variable", "value", "chain")
ggplot(allen_posteriors) + geom_line(aes(index, value)) +
facet_wrap(~ variable, scale="free", ncol=1)
allen_priors <- ddply(allen_posteriors, "variable", function(dd){
grid <- seq(min(dd$value), max(dd$value), length = 100)
data.frame(value = grid, density = par_priors[[dd$variable[1]]](grid))
})
ggplot(allen_posteriors, aes(value)) +
stat_density(geom="path", position="identity", alpha=0.7) +
geom_line(data=allen_priors, aes(x=value, y=density), col="red") +
facet_wrap(~ variable, scale="free", ncol=3)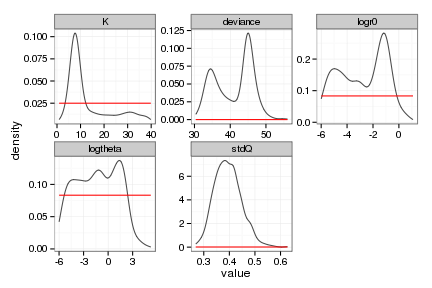
Reshape the posterior parameter distribution data, transform back into original space, and calculate the mean parameters and mean function
A <- allen_posteriors
A$index <- A$index + A$chain * max(A$index) # Combine samples across chains by renumbering index
pardist <- acast(A, index ~ variable)
# pardist <- acast(allen_posteriors[2:3], 1:table(allen_posteriors$variable)[1] ~ variable) # NOT SURE WHY THIS FAILS
# transform model parameters back first
pardist[,"logr0"] = exp(pardist[,"logr0"])
pardist[,"logtheta"] = exp(pardist[,"logtheta"])
colnames(pardist)[colnames(pardist)=="logtheta"] = "theta"
colnames(pardist)[colnames(pardist)=="logr0"] = "r0"
bayes_coef <- apply(pardist,2, posterior.mode)
bayes_pars <- unname(c(bayes_coef["r0"], bayes_coef["K"], bayes_coef["theta"])) # parameters formatted for f
allen_f <- function(x,h,p) unname(RickerAllee(x,h, unname(p[c("r0", "K", "theta")])))
allen_means <- sapply(x_grid, f, 0, bayes_pars)
bayes_pars[1] 0.01929 7.72010 0.06654head(pardist) K deviance r0 theta stdQ
170 21.327 45.03 0.010484 3.826031 0.3737
171 14.261 45.02 0.029587 0.019707 0.4387
172 7.828 40.50 0.129248 2.769482 0.3795
173 29.450 45.66 0.044378 0.006615 0.4461
174 37.580 44.89 0.006334 1.252886 0.3766
175 20.168 45.05 0.033854 0.144171 0.4294Parametric Bayes based on the structurally wrong model (Ricker)
K_prior_p <- c(0.01, 40.0)
logr0_prior_p <- c(-6.0, 6.0)
bugs.model <-
paste(sprintf(
"model{
K ~ dunif(%s, %s)
logr0 ~ dunif(%s, %s)
stdQ ~ dunif(%s, %s)",
K_prior_p[1], K_prior_p[2],
logr0_prior_p[1], logr0_prior_p[2],
stdQ_prior_p[1], stdQ_prior_p[2]),
"
iQ <- 1 / (stdQ * stdQ);
r0 <- exp(logr0)
y[1] ~ dunif(0, 10)
for(t in 1:(N-1)){
mu[t] <- y[t] * exp(r0 * (1 - y[t]/K) )
y[t+1] ~ dnorm(mu[t], iQ)
}
}")
writeLines(bugs.model, "ricker_process.bugs")Compute prior curves
K_prior <- function(x) dunif(x, K_prior_p[1], K_prior_p[2])
logr0_prior <- function(x) dunif(x, logr0_prior_p[1], logr0_prior_p[2])
par_priors <- list(K = K_prior, deviance = function(x) 0 * x,
logr0 = logr0_prior, stdQ = stdQ_prior)We define which parameters to keep track of, and set the initial values of parameters in the transformed space used by the MCMC. We use logarithms to maintain strictly positive values of parameters where appropriate.
# Uniform priors on standard deviation terms
jags.params=c("K","logr0", "stdQ")
jags.inits <- function(){
list("K"=10 * rlnorm(1,0,.5),
"logr0"=log(1) * rlnorm(1,0,.5),
"stdQ"=sqrt(0.05) * rlnorm(1,0,.5),
.RNG.name="base::Wichmann-Hill", .RNG.seed=123)
}
set.seed(12345)
ricker_jags <- do.call(jags.parallel,
list(data=jags.data, inits=jags.inits,
jags.params, n.chains=n.chains,
n.iter=n.iter, n.thin=n.thin, n.burnin=n.burnin,
model.file="ricker_process.bugs"))
recompile(ricker_jags)Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 251
Initializing model
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 251
Initializing model
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 251
Initializing model
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 251
Initializing model
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 251
Initializing model
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 251
Initializing modelricker_jags <- do.call(autojags,
list(object=ricker_jags, n.update=n.update, n.iter=n.iter,
n.thin = n.thin, progress.bar="none"))Convergence diagnostics for parametric bayes Ricker model
tmp <- lapply(as.mcmc(ricker_jags), as.matrix) # strip classes the hard way...
ricker_posteriors <- melt(tmp, id = colnames(tmp[[1]]))
names(ricker_posteriors) = c("index", "variable", "value", "chain")
ggplot(ricker_posteriors) + geom_line(aes(index, value)) +
facet_wrap(~ variable, scale="free", ncol=1)
ricker_priors <- ddply(ricker_posteriors, "variable", function(dd){
grid <- seq(min(dd$value), max(dd$value), length = 100)
data.frame(value = grid, density = par_priors[[dd$variable[1]]](grid))
})
# plot posterior distributions
ggplot(ricker_posteriors, aes(value)) +
stat_density(geom="path", position="identity", alpha=0.7) +
geom_line(data=ricker_priors, aes(x=value, y=density), col="red") +
facet_wrap(~ variable, scale="free", ncol=2)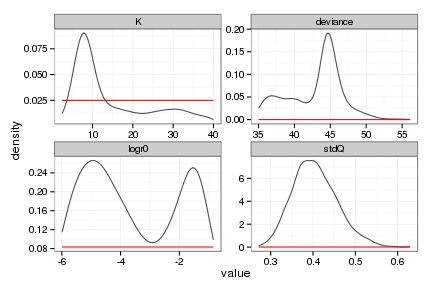
Reshape posteriors data, transform back, calculate mode and corresponding function.
A <- ricker_posteriors
A$index <- A$index + A$chain * max(A$index) # Combine samples across chains by renumbering index
ricker_pardist <- acast(A, index ~ variable)
ricker_pardist[,"logr0"] = exp(ricker_pardist[,"logr0"]) # transform model parameters back first
colnames(ricker_pardist)[colnames(ricker_pardist)=="logr0"] = "r0"
bayes_coef <- apply(ricker_pardist,2, posterior.mode) # much better estimates from mode then mean
ricker_bayes_pars <- unname(c(bayes_coef["r0"], bayes_coef["K"]))
ricker_f <- function(x,h,p){
sapply(x, function(x){
x <- pmax(0, x-h)
pmax(0, x * exp(p["r0"] * (1 - x / p["K"] )) )
})
}
ricker_means <- sapply(x_grid, Ricker, 0, ricker_bayes_pars[c(1,2)])
head(ricker_pardist) K deviance r0 stdQ
170 30.871 44.59 0.011138 0.4164
171 15.920 44.30 0.003492 0.4062
172 8.630 46.04 0.040291 0.4962
173 7.935 37.59 0.172355 0.3977
174 8.622 42.76 0.096497 0.3325
175 8.279 40.48 0.143866 0.4316ricker_bayes_pars[1] 0.008073 8.011228Myers Parametric Bayes
logr0_prior_p <- c(-6.0, 6.0)
logtheta_prior_p <- c(-6.0, 6.0)
logK_prior_p <- c(-6.0, 6.0)
bugs.model <-
paste(sprintf(
"model{
logr0 ~ dunif(%s, %s)
logtheta ~ dunif(%s, %s)
logK ~ dunif(%s, %s)
stdQ ~ dunif(%s, %s)",
logr0_prior_p[1], logr0_prior_p[2],
logtheta_prior_p[1], logtheta_prior_p[2],
logK_prior_p[1], logK_prior_p[2],
stdQ_prior_p[1], stdQ_prior_p[2]),
"
iQ <- 1 / (stdQ * stdQ);
r0 <- exp(logr0)
theta <- exp(logtheta)
K <- exp(logK)
y[1] ~ dunif(0, 10)
for(t in 1:(N-1)){
mu[t] <- r0 * pow(abs(y[t]), theta) / (1 + pow(abs(y[t]), theta) / K)
y[t+1] ~ dnorm(mu[t], iQ)
}
}")
writeLines(bugs.model, "myers_process.bugs")logK_prior <- function(x) dunif(x, logK_prior_p[1], logK_prior_p[2])
logr_prior <- function(x) dunif(x, logr0_prior_p[1], logr0_prior_p[2])
logtheta_prior <- function(x) dunif(x, logtheta_prior_p[1], logtheta_prior_p[2])
par_priors <- list( deviance = function(x) 0 * x, logK = logK_prior,
logr0 = logr_prior, logtheta = logtheta_prior,
stdQ = stdQ_prior)jags.params=c("logr0", "logtheta", "logK", "stdQ")
jags.inits <- function(){
list("logr0"=log(rlnorm(1,0,.1)),
"logK"=log(10 * rlnorm(1,0,.1)),
"logtheta" = log(2 * rlnorm(1,0,.1)),
"stdQ"=sqrt(0.5) * rlnorm(1,0,.1),
.RNG.name="base::Wichmann-Hill", .RNG.seed=123)
}
set.seed(12345)
myers_jags <- do.call(jags.parallel,
list(data=jags.data, inits=jags.inits, jags.params,
n.chains=n.chains, n.iter=n.iter, n.thin=n.thin,
n.burnin=n.burnin, model.file="myers_process.bugs"))
recompile(myers_jags)Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 291
Initializing model
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 291
Initializing model
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 291
Initializing model
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 291
Initializing model
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 291
Initializing model
Compiling model graph
Resolving undeclared variables
Allocating nodes
Graph Size: 291
Initializing modelmyers_jags <- do.call(autojags,
list(myers_jags, n.update=n.update, n.iter=n.iter,
n.thin = n.thin, progress.bar="none"))Convergence diagnostics for parametric bayes
tmp <- lapply(as.mcmc(myers_jags), as.matrix) # strip classes the hard way...
myers_posteriors <- melt(tmp, id = colnames(tmp[[1]]))
names(myers_posteriors) = c("index", "variable", "value", "chain")
ggplot(myers_posteriors) + geom_line(aes(index, value)) +
facet_wrap(~ variable, scale="free", ncol=1)
par_prior_curves <- ddply(myers_posteriors, "variable", function(dd){
grid <- seq(min(dd$value), max(dd$value), length = 100)
data.frame(value = grid, density = par_priors[[dd$variable[1]]](grid))
})
ggplot(myers_posteriors, aes(value)) +
stat_density(geom="path", position="identity", alpha=0.7) +
geom_line(data=par_prior_curves, aes(x=value, y=density), col="red") +
facet_wrap(~ variable, scale="free", ncol=3)
A <- myers_posteriors
A$index <- A$index + A$chain * max(A$index) # Combine samples across chains by renumbering index
myers_pardist <- acast(A, index ~ variable)
### myers_pardist <- acast(myers_posteriors[2:3], 1:table(myers_posteriors$variable) ~ variable)
myers_pardist[,"logK"] = exp(myers_pardist[,"logK"]) # transform model parameters back first
myers_pardist[,"logr0"] = exp(myers_pardist[,"logr0"]) # transform model parameters back first
myers_pardist[,"logtheta"] = exp(myers_pardist[,"logtheta"]) # transform model parameters back first
colnames(myers_pardist)[colnames(myers_pardist)=="logK"] = "K"
colnames(myers_pardist)[colnames(myers_pardist)=="logr0"] = "r0"
colnames(myers_pardist)[colnames(myers_pardist)=="logtheta"] = "theta"
bayes_coef <- apply(myers_pardist,2, posterior.mode) # much better estimates
myers_bayes_pars <- unname(c(bayes_coef[2], bayes_coef[3], bayes_coef[1]))
myers_means <- sapply(x_grid, Myer_harvest, 0, myers_bayes_pars)
myers_f <- function(x,h,p) Myer_harvest(x, h, p[c("r0", "theta", "K")])
head(myers_pardist) deviance K r0 theta stdQ
170 37.69 32.42 0.32913 2.156 0.2818
171 32.99 51.72 0.20896 2.373 0.3612
172 40.26 52.83 0.22398 2.260 0.4654
173 32.80 76.54 0.12968 2.749 0.3711
174 32.81 216.04 0.04136 3.512 0.3907
175 32.55 330.07 0.02654 3.813 0.3118myers_bayes_pars[1] 31.8192 0.1065 34.4760Phase-space diagram of the expected dynamics
models <- data.frame(x=x_grid,
GP=tgp_dat$y,
True=true_means,
MLE=est_means,
Ricker=ricker_means,
Allen = allen_means,
Myers = myers_means)
models <- melt(models, id="x")
# some labels
names(models) <- c("x", "method", "value")
# labels for the colorkey too
model_names = c("GP", "True", "MLE", "Ricker", "Allen", "Myers")
colorkey=cbPalette
names(colorkey) = model_names plot_gp <- ggplot(tgp_dat) + geom_ribbon(aes(x,y,ymin=ymin,ymax=ymax), fill="gray80") +
geom_line(data=models, aes(x, value, col=method), lwd=1, alpha=0.8) +
geom_point(data=obs, aes(x,y), alpha=0.8) +
xlab(expression(X[t])) + ylab(expression(X[t+1])) +
scale_colour_manual(values=cbPalette)
print(plot_gp)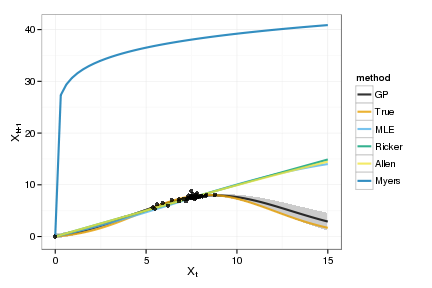
Goodness of fit
This shows only the mean predictions. For the Bayesian cases, we can instead loop over the posteriors of the parameters (or samples from the GP posterior) to get the distribution of such curves in each case.
require(MASS)
step_ahead <- function(x, f, p){
h = 0
x_predict <- sapply(x, f, h, p)
n <- length(x_predict) - 1
y <- c(x[1], x_predict[1:n])
y
}
step_ahead_posteriors <- function(x){
gp_f_at_obs <- gp_predict(gp, x, burnin=1e4, thin=300)
df_post <- melt(lapply(sample(100),
function(i){
data.frame(time = 1:length(x), stock = x,
GP = mvrnorm(1, gp_f_at_obs$Ef_posterior[,i], gp_f_at_obs$Cf_posterior[[i]]),
True = step_ahead(x,f,p),
MLE = step_ahead(x,f,est$p),
Allen = step_ahead(x, allen_f, pardist[i,]),
Ricker = step_ahead(x, ricker_f, ricker_pardist[i,]),
Myers = step_ahead(x, myers_f, myers_pardist[i,]))
}), id=c("time", "stock"))
}
df_post <- step_ahead_posteriors(x)
ggplot(df_post) + geom_point(aes(time, stock)) +
geom_line(aes(time, value, col=variable, group=interaction(L1,variable)), alpha=.1) +
scale_colour_manual(values=colorkey, guide = guide_legend(override.aes = list(alpha = 1))) 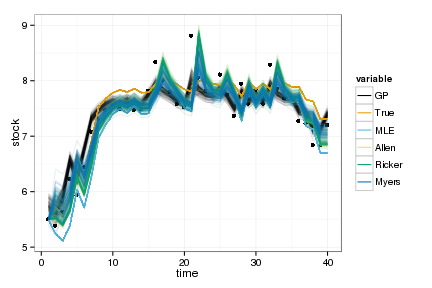
Optimal policies by value iteration
Compute the optimal policy under each model using stochastic dynamic programming. We begin with the policy based on the GP model,
MaxT = 1000
# uses expected values from GP, instead of integrating over posterior
#matrices_gp <- gp_transition_matrix(gp_dat$E_Ef, gp_dat$E_Vf, x_grid, h_grid)
# Integrate over posteriors
matrices_gp <- gp_transition_matrix(gp_dat$Ef_posterior, gp_dat$Vf_posterior, x_grid, h_grid)
# Solve the SDP using the GP-derived transition matrix
opt_gp <- value_iteration(matrices_gp, x_grid, h_grid, MaxT, xT, profit, delta, reward)Determine the optimal policy based on the allen and MLE models
matrices_true <- f_transition_matrix(f, p, x_grid, h_grid, sigma_g)
opt_true <- value_iteration(matrices_true, x_grid, h_grid, OptTime=MaxT, xT, profit, delta=delta)
matrices_estimated <- f_transition_matrix(est$f, est$p, x_grid, h_grid, est$sigma_g)
opt_estimated <- value_iteration(matrices_estimated, x_grid, h_grid, OptTime=MaxT, xT, profit, delta=delta)Determine the optimal policy based on Bayesian Allen model
matrices_allen <- parameter_uncertainty_SDP(allen_f, x_grid, h_grid, pardist, 4)
opt_allen <- value_iteration(matrices_allen, x_grid, h_grid, OptTime=MaxT, xT, profit, delta=delta)Bayesian Ricker
matrices_ricker <- parameter_uncertainty_SDP(ricker_f, x_grid, h_grid, as.matrix(ricker_pardist), 3)
opt_ricker <- value_iteration(matrices_ricker, x_grid, h_grid, OptTime=MaxT, xT, profit, delta=delta)Bayesian Myers model
matrices_myers <- parameter_uncertainty_SDP(myers_f, x_grid, h_grid, as.matrix(myers_pardist), 4)
myers_alt <- value_iteration(matrices_myers, x_grid, h_grid, OptTime=MaxT, xT, profit, delta=delta)Assemble the data
OPT = data.frame(GP = opt_gp$D, True = opt_true$D, MLE = opt_estimated$D, Ricker = opt_ricker$D, Allen = opt_allen$D, Myers = myers_alt$D)
colorkey=cbPalette
names(colorkey) = names(OPT) Graph of the optimal policies
policies <- melt(data.frame(stock=x_grid, sapply(OPT, function(x) x_grid[x])), id="stock")
names(policies) <- c("stock", "method", "value")
ggplot(policies, aes(stock, stock - value, color=method)) +
geom_line(lwd=1.2, alpha=0.8) + xlab("stock size") + ylab("escapement") +
scale_colour_manual(values=colorkey)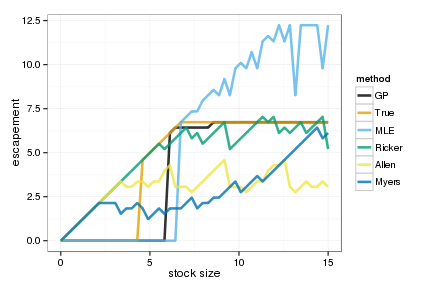
Simulate 100 realizations managed under each of the policies
sims <- lapply(OPT, function(D){
set.seed(1)
lapply(1:100, function(i)
ForwardSimulate(f, p, x_grid, h_grid, x0, D, z_g, profit=profit, OptTime=OptTime)
)
})
dat <- melt(sims, id=names(sims[[1]][[1]]))
dt <- data.table(dat)
setnames(dt, c("L1", "L2"), c("method", "reps"))
# Legend in original ordering please, not alphabetical:
dt$method = factor(dt$method, ordered=TRUE, levels=names(OPT))ggplot(dt) +
geom_line(aes(time, fishstock, group=interaction(reps,method), color=method), alpha=.1) +
scale_colour_manual(values=colorkey, guide = guide_legend(override.aes = list(alpha = 1)))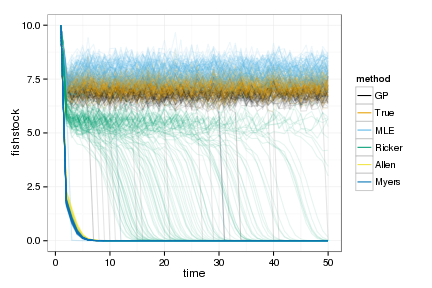
Profit <- dt[, sum(profit), by=c("reps", "method")]
Profit[, mean(V1), by="method"] method V1
1: GP 24.908
2: True 26.532
3: MLE 4.420
4: Ricker 8.363
5: Allen 7.041
6: Myers 7.347ggplot(Profit, aes(V1)) + geom_histogram() +
facet_wrap(~method, scales = "free_y") + guides(legend.position = "none") + xlab("Total profit by replicate")
allen_deviance <- posterior.mode(pardist[,'deviance'])
ricker_deviance <- posterior.mode(ricker_pardist[,'deviance'])
myers_deviance <- posterior.mode(myers_pardist[,'deviance'])
true_deviance <- 2*estf(c(p, sigma_g))
mle_deviance <- 2*estf(c(est$p, est$sigma_g))
c(allen = allen_deviance, ricker=ricker_deviance, myers=myers_deviance, true=true_deviance, mle=mle_deviance) allen ricker myers true mle
45.26 44.78 34.48 -61.08 -287.60