Gaussian process inference on sample functions

• This example uses the direct inversion of the covariance function. I have also been exploring the potentially faster Cholksy decomposition without success. Sometimes the match is very good, other times not, see compare-cholsky.md
• This example also on github as reed-example.md.
  
• Basic likelihood optimization needs to be checked. See commits estimating sigma_n and estimating l. Compare the example below to a different set of fixed hyperparameters here

Example

require(pdgControl)
require(ggplot2)

Simulate some training data under a stochastic growth function with standard parameterization,

f <- BevHolt
p <- c(1.5, 0.05)
K <- (p[1] - 1)/p[2]

Noise function

z_g <- function(sigma_g) rlnorm(1, 0, sigma_g)  #1+(2*runif(1, 0,  1)-1)*sigma_g #

Parameter definitions

x_grid = seq(0, 1.5 * K, length = 100)
T <- 40
sigma_g <- 0.1
x <- numeric(T)
x[1] <- 1

Simulation

for (t in 1:(T - 1)) x[t + 1] = z_g(sigma_g) * f(x[t], h = 0, p = p)

plot(x)

Predict the function over the target grid

obs <- data.frame(x = x[1:(T - 1)], y = x[2:T])
X <- x_grid
library(nonparametricbayes)
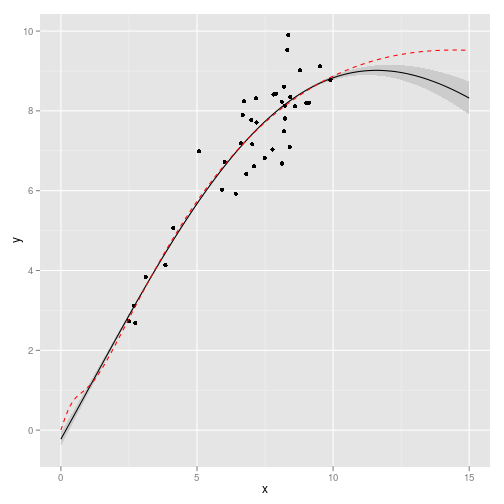
gp <- gp_fit(obs, X, c(sigma_n = 0.05, l = 10))

Gaussian Process inference from this model. True model shown in red.

df <- data.frame(x = X, y = gp$Ef, ymin = (gp$Ef - 2 * sqrt(abs(diag(gp$Cf)))), 
    ymax = (gp$Ef + 2 * sqrt(abs(diag(gp$Cf)))))
true <- data.frame(x = X, y = sapply(X, f, 0, p))
require(ggplot2)
ggplot(df) + geom_ribbon(aes(x, y, ymin = ymin, ymax = ymax), fill = "gray80") + 
    geom_line(aes(x, y)) + geom_point(data = obs, aes(x, y)) + geom_line(data = true, 
    aes(x, y), col = "red", lty = 2)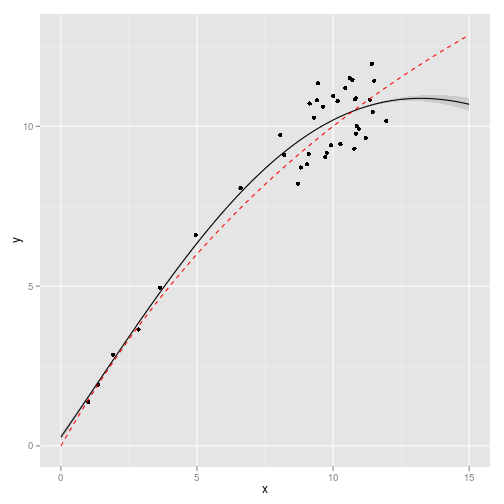

Another example using the May model

f <- May
p <- c(r = 0.75, k = 10, a = 1.2, H = 1, Q = 3)
K <- 8  # approx

Model dynamics look like this:

birth <- function(x) p["r"] * (1 - x/p["k"])
death <- function(x) p["a"] * x^(p["Q"] - 1)/(x^p["Q"] + p["H"])
df <- data.frame(x = x_grid, b = sapply(x_grid, birth), d = sapply(x_grid, 
    death))
ggplot(df) + geom_line(aes(x, b), col = "blue") + geom_line(aes(x, 
    d), col = "red")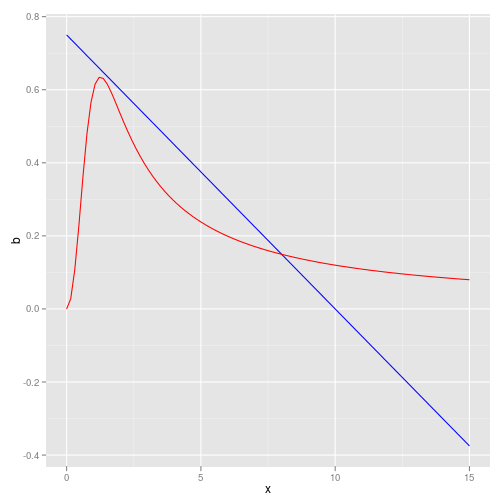

Simulation

x[1] = 2.5
for (t in 1:(T - 1)) x[t + 1] = z_g(sigma_g) * f(x[t], h = 0, p = p)
plot(x)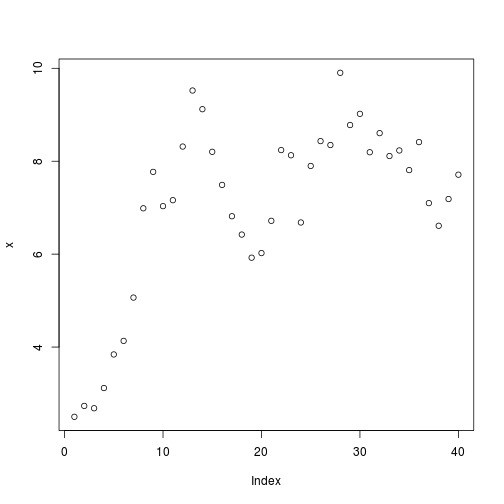

Predict the function over the target grid

obs <- data.frame(x = x[1:(T - 1)], y = x[2:T])
X <- x_grid
library(nonparametricbayes)
gp <- gp_fit(obs, X, c(sigma_n = 0.05, l = 10))

Gaussian Process inference from this model

df <- data.frame(x = X, y = gp$Ef, ymin = (gp$Ef - 2 * sqrt(abs(diag(gp$Cf)))), 
    ymax = (gp$Ef + 2 * sqrt(abs(diag(gp$Cf)))))
true <- data.frame(x = X, y = sapply(X, f, 0, p))
ggplot(df) + geom_ribbon(aes(x, y, ymin = ymin, ymax = ymax), fill = "gray80") + 
    geom_line(aes(x, y)) + geom_point(data = obs, aes(x, y)) + geom_line(data = true, 
    aes(x, y), col = "red", lty = 2)