Comparing numerical methods

require(MASS)
require(ggplot2)
require(kernlab)

Parameterization-specific

X <- seq(-5,5,len=50)
obs <- data.frame(x = c(-4, -3, -1,  0,  2),
                  y = c(-2,  0,  1,  2, -1))
l <- 1
sigma_n <- 0.8

Radial basis function/Gaussian kernel:

  SE <- function(Xi,Xj, l) exp(-0.5 * (Xi - Xj) ^ 2 / l ^ 2)
  cov <- function(X, Y) outer(X, Y, SE, l)

Cholksy method

  n <- length(obs$x)
  K <- cov(obs$x, obs$x)
  I <-  diag(1, n)

  L <- chol(K + sigma_n^2 * I)
  alpha <- solve(t(L), solve(L, obs$y))
  k_star <- cov(obs$x, X)
  Y <- t(k_star) %*% alpha
  v <- solve(L, k_star)
  Var <- cov(X,X) - t(v) %*% v
  loglik <- -.5 * t(obs$y) %*% alpha - sum(log(diag(L))) - n * log(2 * pi) / 2

Direct method

  cov_xx_inv <- solve(K + sigma_n^2*I)
  Ef <- cov(X, obs$x) %*% cov_xx_inv %*% obs$y
  Cf <- cov(X, X) - cov(X, obs$x)  %*% cov_xx_inv %*% cov(obs$x, X)
gp <- gausspr(obs$x, obs$y, kernel="rbfdot", kpar=list(sigma=1/(2*l^2)), fit=FALSE, scaled=FALSE, var=0.8)
y_p <- predict(gp, X)

Things that should be equivelent but aren’t quite:

ggplot(data.frame(x=X, Ef=Ef, Y=Y, y_p = y_p))+ geom_point(aes(x,Ef), col='red') + geom_point(aes(x,Y)) + geom_line(aes(x,y_p))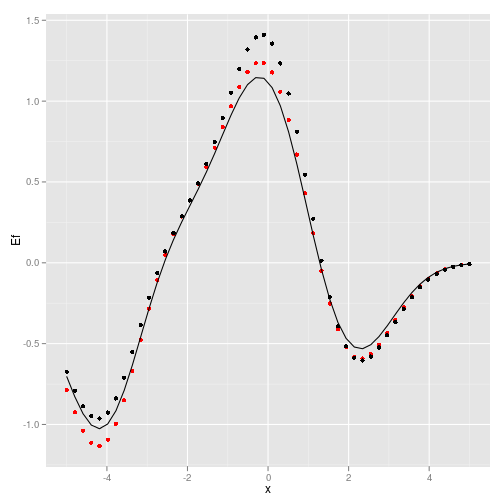
plot of chunk unnamed-chunk-8
plot of chunk unnamed-chunk-8
cov_xx_inv %*% obs$y
        [,1]
[1,] -1.4059
[2,]  0.5010
[3,]  0.1288
[4,]  1.2275
[5,] -0.7119
alpha
[1] -1.21293  0.46074  0.07548  1.44144 -0.73949
alpha(gp)
        [,1]
[1,] -1.2475
[2,]  0.4011
[3,]  0.1661
[4,]  1.1010
[5,] -0.6394