Noam gave an interesting presentation in our lab today, prompted me to do a little experimentation. Weakening stability across a set of coupled patches should result in increased autocorrelation. Decided to test this with a little visualization with help of a quick R script. 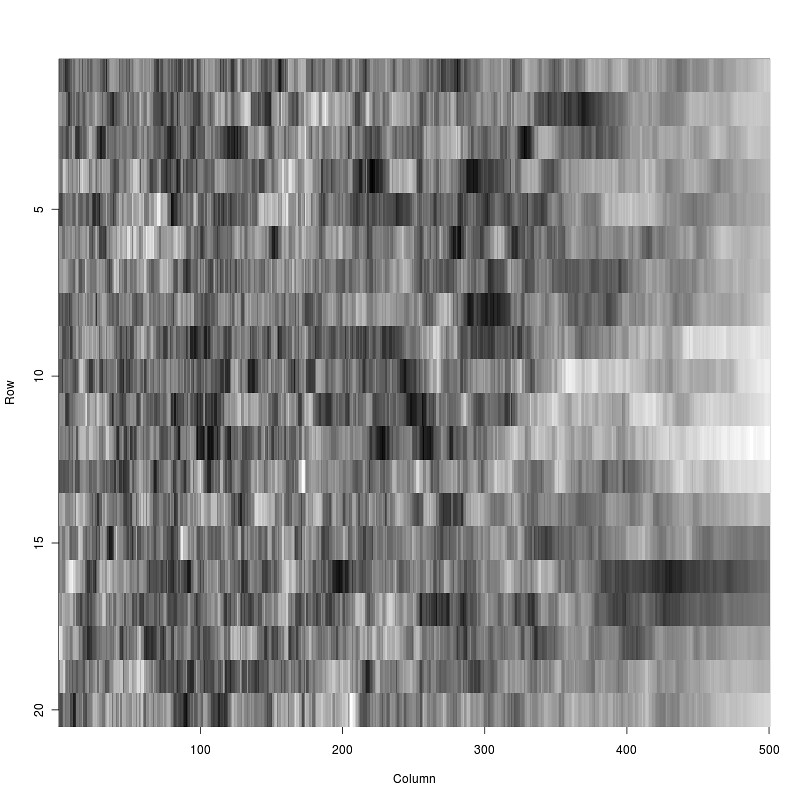
Time progresses across the x-axis, 1-D space (on S1) across the y-axis. Each patch suffers a slow loss of stability, resulting in a clearly visible increase in autocorrelation.
Power in Warning Signals
Meanwhile, returning to my work with power in warning signals. Working on a more complete analytical description of the underlying saddle node bifurcation in the example to justify having the “true” underlying model. First, a quick script for the (larger) analytic equilibrium as a function of the bifurcation parameter. From this we can calculate the change in the eigenvalue at the equilibrium as we approach the bifurcation: (code here: saddle_analytics.R)
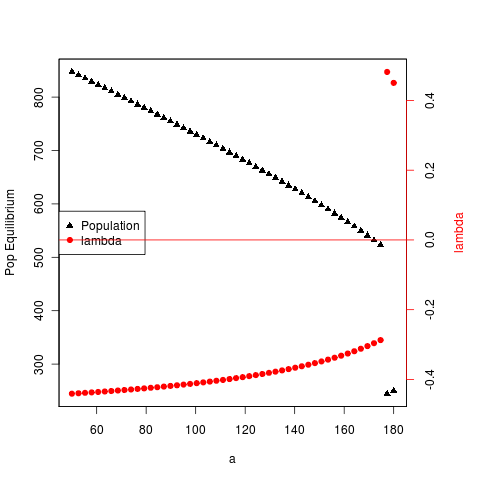
Note that the eigenvalue lambda is evaluated at the fixed point in each case, and over sufficient range in the bifurcation parameter, the change is non-linear. The bifurcation seems to happen at about \(a=174\), corresponding to an equilibrium population of \(\hat x = 525\). lambda doesn’t depend on the bifurcation parameter \[a\] except through the value of \(\hat x\); Unfortunately closed form expressions for \(\frac{e K x^2}{h^2+x^2}-e x - a = 0\) aren’t particularly manageable. The jump in \(\hat x\) which results in a jump in lambda is the result of the numerical minimizer starting to grab the other root – of course lambda should in fact pass smoothly through zero, triggering the bifurcation.
and in the literature…
Just noticed anintriguing paper by R. M. Bailey on warning signals applied to a spatial simulation (cellular automata model). Appears to focus on classical indicators methods, without discussion of statistical inference or spatially based warning signals. Also, the bifurcation model is unclear to me, seems that some effects are rather related to changing the timescale (effectively the birth rate in this case?) of the model, not necessarily the stability. The need for non-dimensionalization strikes again. Finally, the question of perturbations into alternative stable states continues to be blended into discussions about critical slowing down and bifurcations. While the latter makes the former more likely, the rather different mechanisms by which each drives change seem conflated.