I consider the optimal stochastic-dynamic programming solution for the model specified with known stochasticity in population dynamics, but now vary the actual simulated dynamics to include further uncertainty or error not included in the optimal solution in different ways. In some way this is an “unfair” analysis, as I really should be solving for the optimal solution in light of the fully uncertain space, but in practice this at least serves as a sensitivity analysis to the assumptions that certain quantities are perfectly known. I consider several scenarios below.
Parameter value misspecification
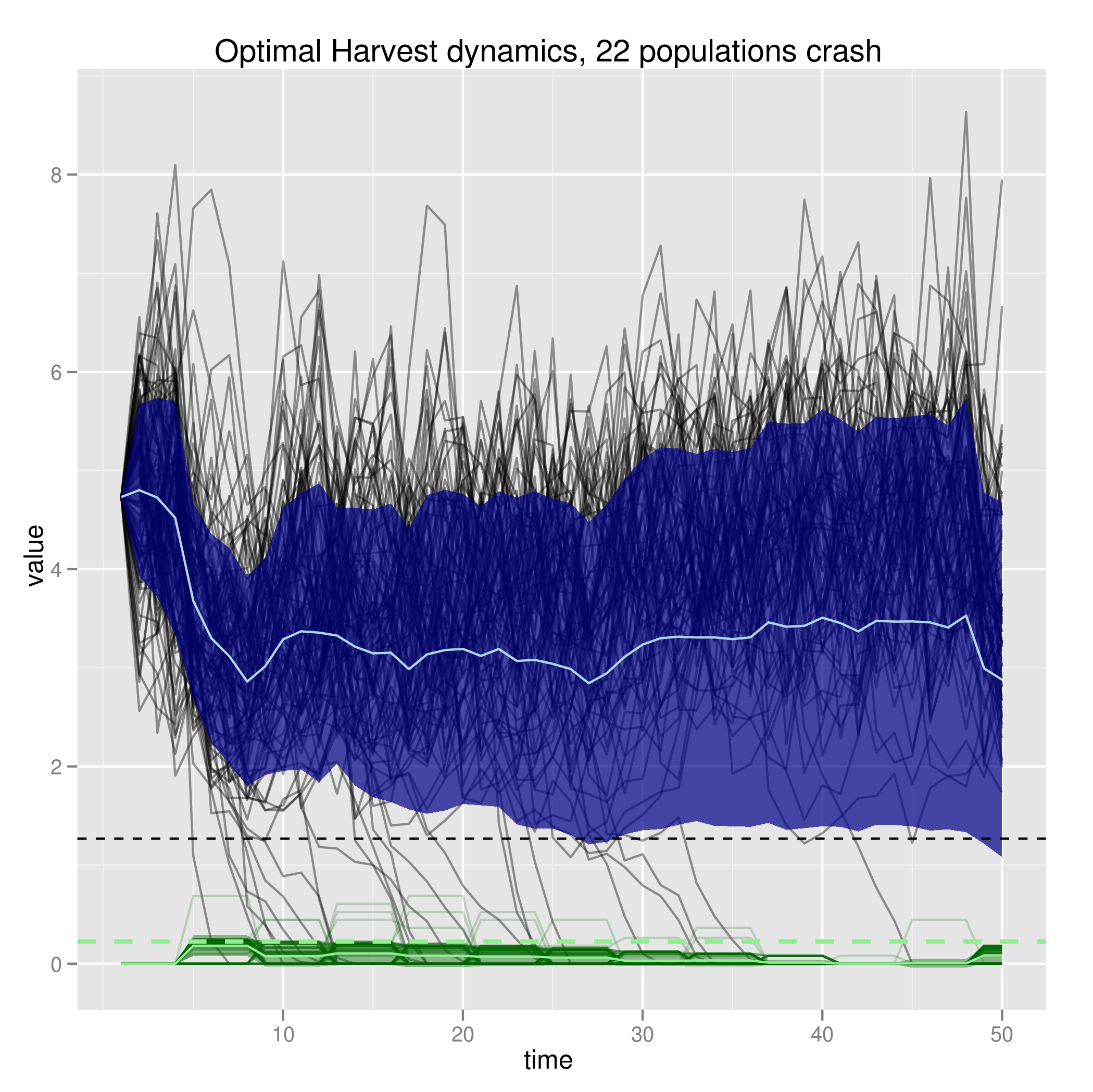
Has essentially no impact on extinction risk on models without allee effects, but dramatic impact of 5% overestimate in a parameter. Many optimally managed populations crash, compare to very few crashes of the same dynamics in unharvested scenario:
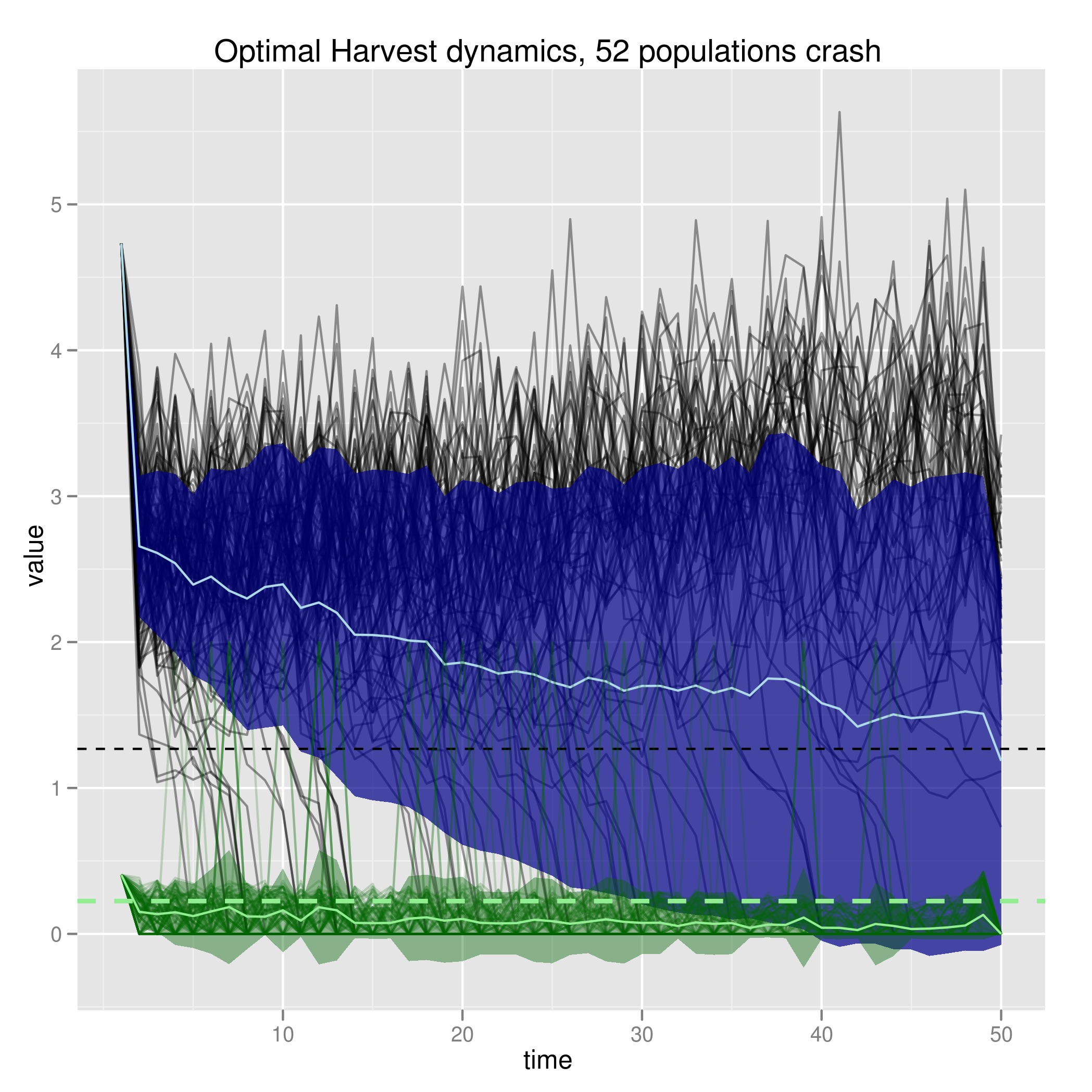
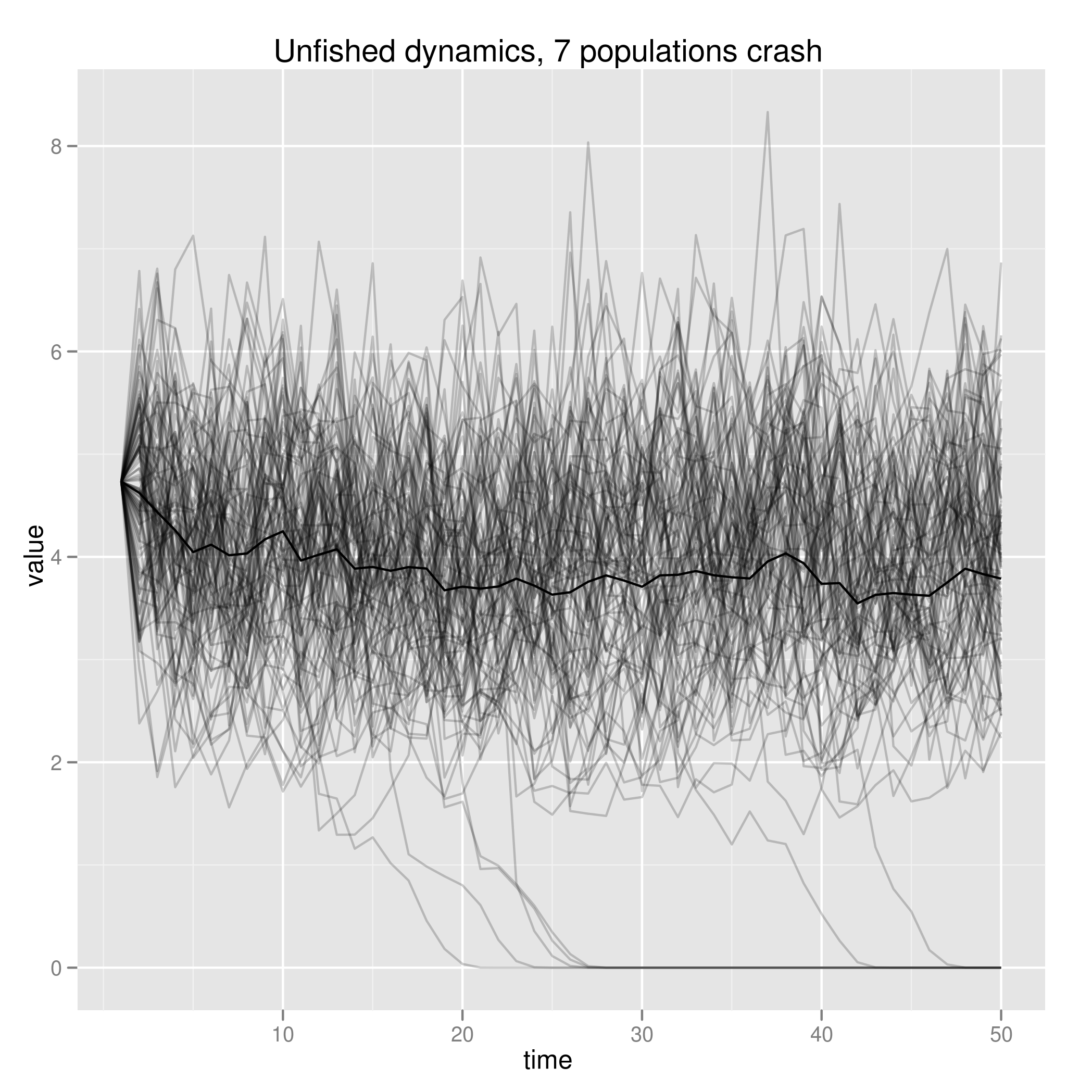
Uncertainty in harvest and stock
Doing optimal management that accounts for stock growth uncertainty but not harvest uncertainty or stock assessment uncertainty. Large stock assessment uncertainty can crash even the non-allee Beverton-Holt model.
Risk of ignoring stock-assessment uncertainty
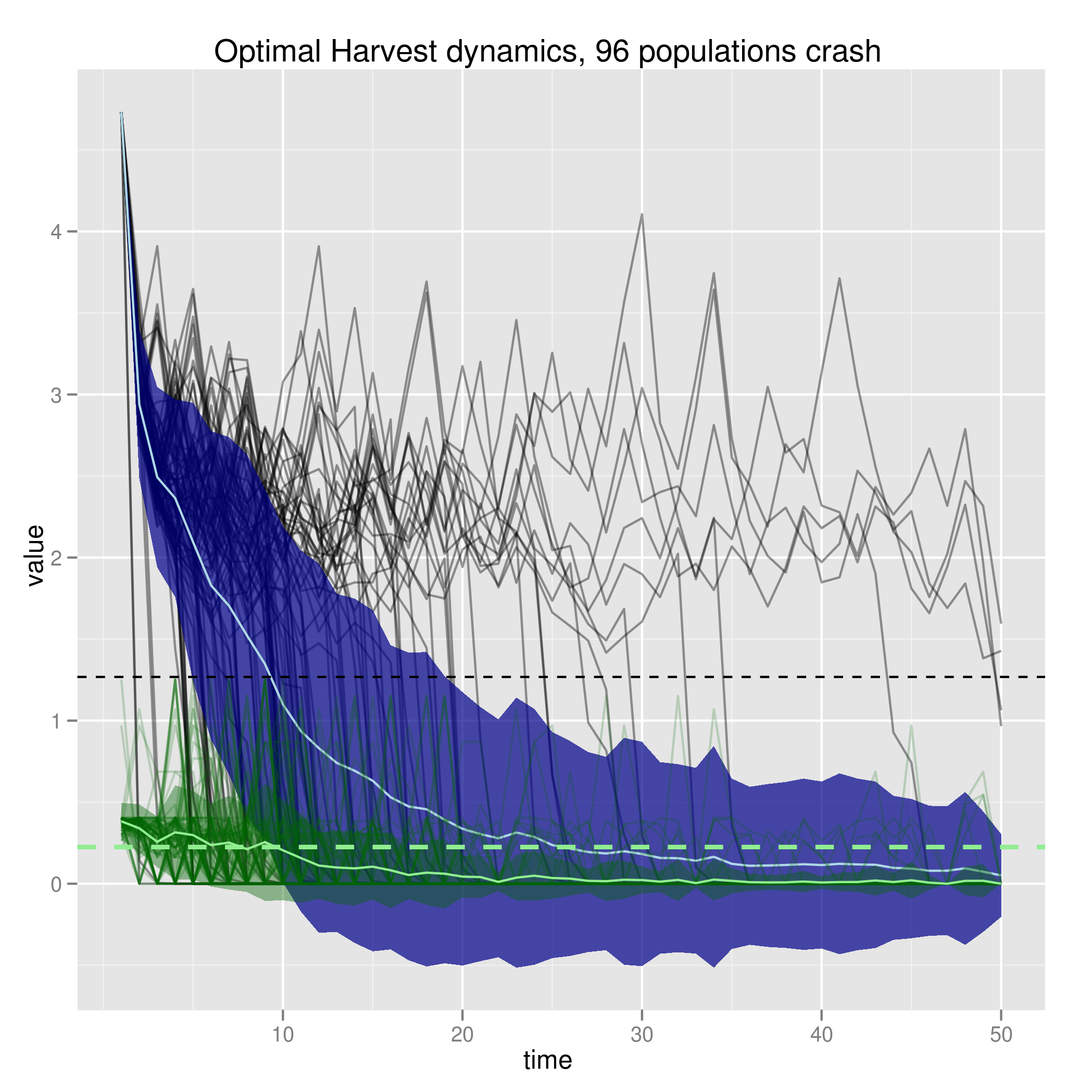
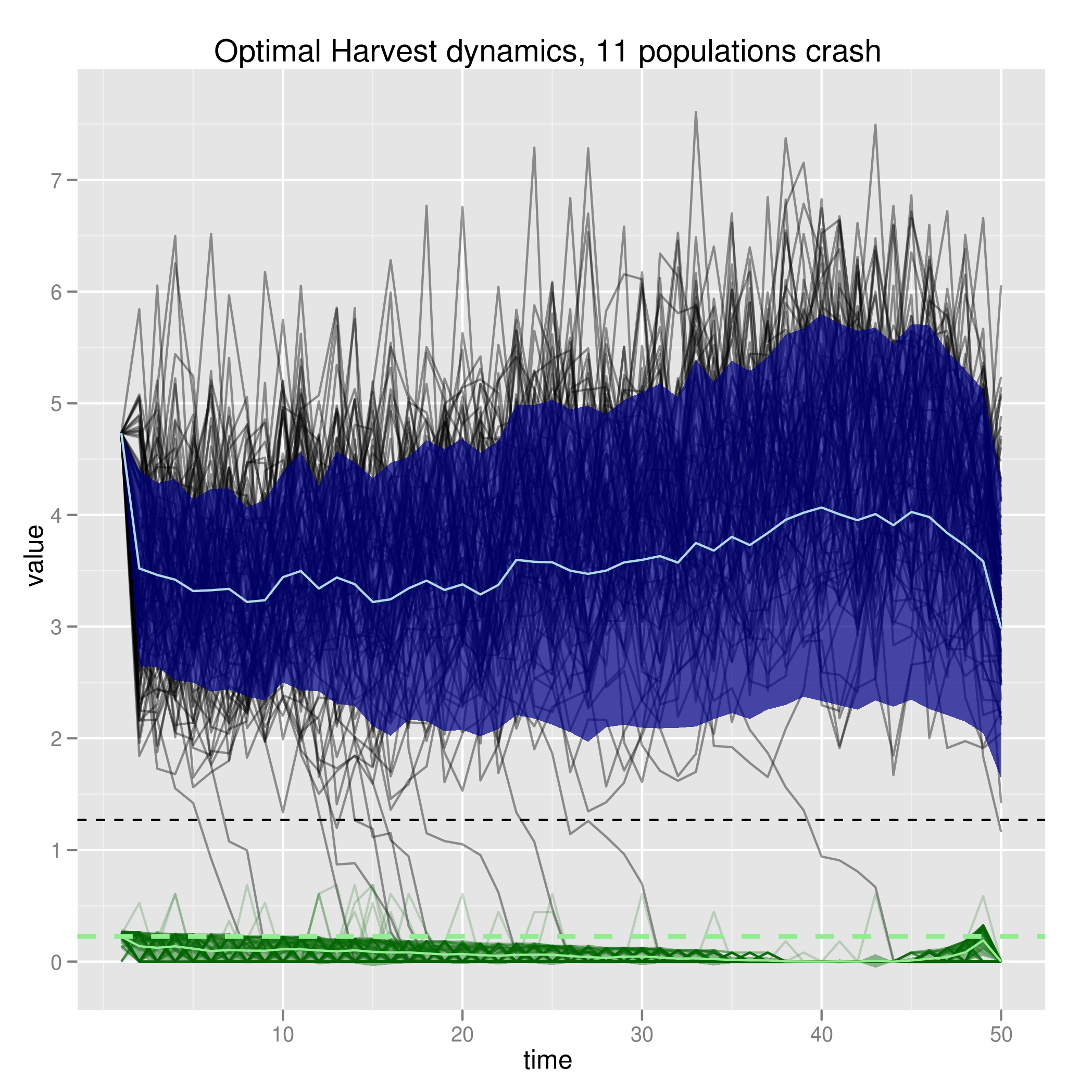
Will need to account for these uncertainties in the optimal solution. Increasing noise in the population dynamics (which the optimal solution is compensating for) can compensate for this, and additional stock assessment noise doesn’t do much additional damage:
Unaccounted-for uncertainty can have little impact when smaller than the accounted-for sources
including policy limitations
Consider performing the stock assessment and updating the harvest quota (according to the optimal management solution) every four years. Note this is suboptimal as the optimization assumed updating every year was possible.

further simple examples
Should consider annually adjusted quotas based on projected stock assessment. Compare to fixed quota calculated for a 4-yr interval between assessments.
Slower-responding policy variable? cost to changing fishing effort? differential cost to increase vs decrease effort? differing timescales?
Should add plots to compare profits associated with different perturbations
Varying the cost of extinction
This one is a bit different then the uncertainty experiments. Since the population can crash, we can consider a penalty for crashing the population by offering a reward for meeting the boundary condition. In the deterministic (or nearly deterministic) case, this condition is always satisfied. In the very stochastic case, the optimal solution accepts some probability of not satisfying the boundary condition in return for a greater harvest reward.
Dramatically (100x) increasing reward for meeting boundary condition at or above allee threshold can decrease crashes even in spite of model parameter misspecification (5% lower growth, as above):

Direct (but finite) cost penalty on extinction, vs adjusting reward for meeting boundary condition? How is this implemented?
Learning & adaptive management
Reading/Refs
Working through Sethi et al, “Fishery Management Under Multiple Uncertainty,” (Sethi et. al. 2005)
References
- Sethi G, Costello C, Fisher A, Hanemann M and Karp L (2005). “Fishery Management Under Multiple Uncertainty.” Journal of Environmental Economics And Management, 50. ISSN 00950696, https://dx.doi.org/10.1016/j.jeem.2004.11.005.