The overnight runs yesterday using the geiger models bm and lambda on the (transformed) Anoles dataset don’t seem to converge, spooling jobs that continue running even when R exits – probably that same problem in ape somewhere that was fixed by writing the tree out to Nexus and re-reading it, a very strange and subtle bug. Will try this and restart the runs.
Ordered as: bm_v_lambda_origdata.png, delta_v_lambda.png, bm_v_lambda.png (data simulated under OU), each with 100 replicates.
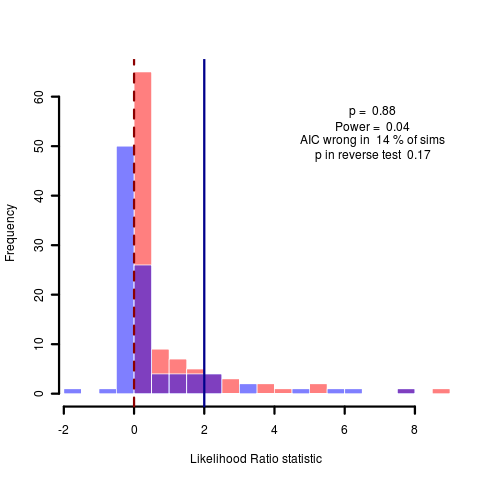


Clearly difficult to distinguish in the first two cases, as expected given the parameter values under this transformation. The third case is under simulated data with an alpha of 2, but the data estimates a lambda very near unity (0.98), so again this isn’t surprising. Re-estimating by simulating new data under the same model, we fit a lambda of 0.55, now AIC at least favors the lambda model and we repeat the Monte Carlo and get more conclusive difference between models, as expected:

Thus while we can distinguish between models of different lambda reasonably well under the Monte Carlo framework, we cannot initially estimate reasonably parameterized models of lambda. Even the power curve seems not to give an indication that the initial estimate of lambda by maximum likelihood is not to be trusted. Will have to think about this relatively obvious source of uncertainty, maybe better to just draw from the distribution of lambda values appropriately in the monte carlo, rather than generating all simulations from the MLE estimate.
Geospiza data examples
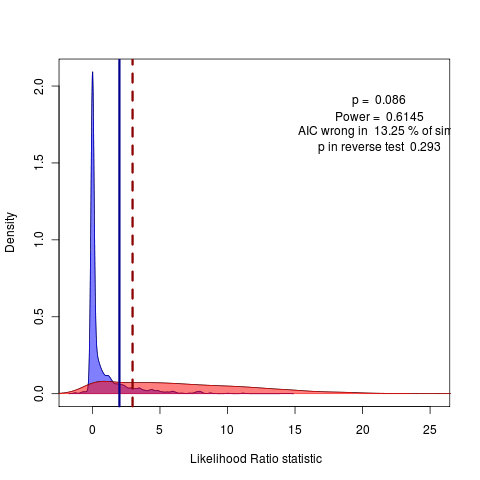
Going back to Geiger geospiza dataset on wing length, just ran 2000 replicates on Monte Carlo of lambda vs delta model:
Slow code, New tact
Meanwhile still frustrated with the speed of Geiger for these applications. In particular, solving the Brownian rate parameter problem is the solution to a linear equation, and shouldn’t need nonlinear optimization. OUCH implements a linear solver for brown() function. Would be possible to wrap a search for a tree transformation around this, optimizing the sigma for each trial version of the optimization, rather than treating this as a non-linear optimization of two parameters simultaneously.
Note that this is already done for the mean of the Brownian model even in Geiger, where it is taken as the Phylogenetic mean from the tree, so only sigma (which geiger sometimes calls beta, or is beta equal sigma sqaured??) is fitted.
Using the gsl library I’ve written my own likelihood calculations for BM and OU models, linearsoln.c, should probably re-implement into wrightscape(?)