I compare in a robust framework the likelihood that species mean trait values are generated by Brownian motion, a single peak OU model, or a model with different regimes (postulated in the literature) in which the selective strength (alpha) and diversification rate (sigma) are fixed across the entire tree or allowed to vary by selective regime. (Regimes are defined as branches with different values for the selective optimum).
The parametric bootstrap of the likelihood ratio statistic provides a rigorous way to quantify the probability that the model choice is correct: the probability that the data was produced by the test model vs the null model is assured by the Neyman-Pearson lemma. Because the models are nested in a natural hierarchy, pairwise tests of successively more complicated models provide an efficient and robust way to select between models, whereas other methods may be misleading.
Anoles Data
OU cannot reject BM, OU.LP (three peaks) can reject OU single peak model (and hence BM). Allowing alpha and sigma to vary by regime shows an improvement better then expected by chance under the global alpha/sigma model 93% of the time, which we may take as insufficient justification of the separate strengths of selection and diversification between regimes.


require(wrightscape)
data(bimac)
tree <- with(bimac,ouchtree(nodes=node,ancestors=ancestor,times=time/max(time),labels=species))
bm <- brown(log(bimac['size']), tree)
ou1 <- hansen(log(bimac['size']), tree, bimac['OU.1'], 1, 1)
ws1 <- wrightscape(log(bimac['size']), tree, bimac['OU.1'], 1, 1)
ou2 <- hansen(log(bimac['size']), tree, bimac['OU.LP'], 1, 1)
ws2 <- wrightscape(log(bimac['size']), tree, bimac['OU.LP'], ([email protected])^2, ou2@sigma)
model_list <- list(bm = bm, ws1 = ws1, ou2 = ou2, ws2 = ws2)
LR <- choose_model(model_list, 100)
png("wrightscape_anoles.png", width = 2000, height=600)
par(mfrow=c(1,3))
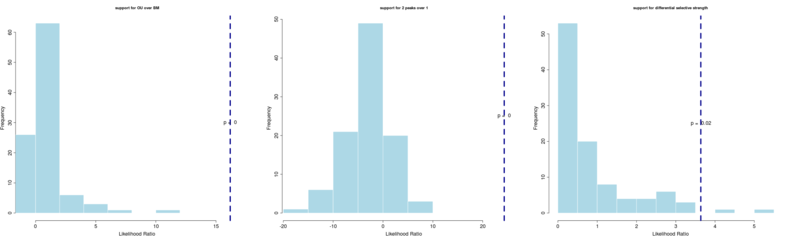
pretty_plot(LR[[1]], main="support for OU over BM")
pretty_plot(LR[[2]], main="support for multiple peaks over 1")
pretty_plot(LR[[3]], main="support for differential selective strength")
dev.off()
### Sedges Data
OU model clearly rejects BM, two regimes clearly rejects the single OU peak, and separate selective regimes appears supported at the p = 0.02 level.

require(wrightscape)
require(maticce)
data(carex)
attach(carex)
treedata <- ape2ouch_all(ovales.tree, ovales.data)
ou2_regimes <- paintBranches(list(ovales.nodes[[2]]), treedata$tree)
ou1_regimes <- as.factor(rep(1, length(ou2_regimes) ))
names(ou1_regimes) <- names(ou2_regimes)
# Fit the models
bm <- brown(treedata$data, treedata$tree)
ws1 <- wrightscape(treedata$data, treedata$tree, ou1_regimes, 1, 1)
ou2 <- hansen(treedata$data, treedata$tree, ou2_regimes, 1, 1)
ws2 <- wrightscape(treedata$data, treedata$tree, ou2_regimes, ([email protected])^2, ou2@sigma)
model_list <- list(bm = bm, ws1 = ws1, ou2 = ou2, ws2 = ws2)
LR <- choose_model(model_list, 100)
pretty_plot(LR[[1]], main="support for OU over BM")
pretty_plot(LR[[2]], main="support for 2 peaks over 1")
pretty_plot(LR[[3]], main="support for differential selective strength")Significant code changes
Fixed handling of out-of-bounds parameters. Used to just write in the boundary size whenever the algorithm tried to go outside the boundary, which essentially breaks the algorithm. Now it returns a minus log likelihood of infinity (GSL_POSINF) instead, which seems to greatly improve the observed performance of the algorithm.
Should have a way to indicate whether negative values are appropriate or not for theta parameters!
Simplex method convergence – still struggles with parameter rich models. During bootstrapping a substantial number of runs will hit the maximum number of iterations. Increased to 20,000 iterations and relaxed error tolerance to 1e-6, which seems to mostly fix this. Method should probably throw a warning when it hits the maximum iterations though.
Optimization
- Appropriate treatment for root parameter?
- appropriate handling for parameter boundaries?
simulated annealing vs simplex method
Add back the fast method for single regime
parameter global/local controls
R level control of search algorithm parameters