Large Intrinsic Noise

Modified Crowley model

Realizing Arbitrarily large demographic noise systems??

Consider the Crowley model from last week which I’d implemented as an individual birth-death model: (x is the better competitor, y the better colonist)

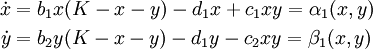
\begin{align} \dot x &= b_1 x (K - x - y) - d_1 x + c_1 x y = \alpha_1(x,y) \\ \dot y &= b_2 y (K - x - y) - d_1 y - c_2 x y = \beta_1(x,y) \end{align}
\begin{align} \dot x &= b_1 x (K - x - y) - d_1 x + c_1 x y = \alpha_1(x,y) \\ \dot y &= b_2 y (K - x - y) - d_1 y - c_2 x y = \beta_1(x,y) \end{align}

I’ve implemented the linear noise approximation for this model as a system of coupled ODEs:

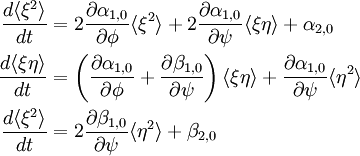
\begin{align} \frac{d \langle \xi^2 \rangle}{d t} &= 2 \frac{\partial \alpha_{1,0}}{\partial \phi} \langle \xi^2 \rangle + 2 \frac{\partial \alpha_{1,0} }{\partial \psi} \langle \xi \eta \rangle + \alpha_{2,0} \\ \frac{d \langle \xi \eta \rangle}{d t} &= \left( \frac{\partial \alpha_{1,0}}{\partial \phi} + \frac{\partial \beta_{1,0} }{\partial \psi} \right)\langle \xi \eta \rangle+ \frac{\partial \alpha_{1,0} }{\partial \psi} \langle \eta^2 \rangle \\ \frac{d \langle \xi^2 \rangle}{d t} &= 2 \frac{\partial \beta_{1,0}}{\partial \psi} \langle \eta^2 \rangle + \beta_{2,0} \end{align}
\begin{align} \frac{d \langle \xi^2 \rangle}{d t} &= 2 \frac{\partial \alpha_{1,0}}{\partial \phi} \langle \xi^2 \rangle + 2 \frac{\partial \alpha_{1,0} }{\partial \psi} \langle \xi \eta \rangle + \alpha_{2,0} \\ \frac{d \langle \xi \eta \rangle}{d t} &= \left( \frac{\partial \alpha_{1,0}}{\partial \phi} + \frac{\partial \beta_{1,0} }{\partial \psi} \right)\langle \xi \eta \rangle+ \frac{\partial \alpha_{1,0} }{\partial \psi} \langle \eta^2 \rangle \\ \frac{d \langle \xi^2 \rangle}{d t} &= 2 \frac{\partial \beta_{1,0}}{\partial \psi} \langle \eta^2 \rangle + \beta_{2,0} \end{align}

And solved numerically (R code, links directly to this version and can run stand-alone from the package) using parameter values matching the individual based simulation (C code from warning_signals package).

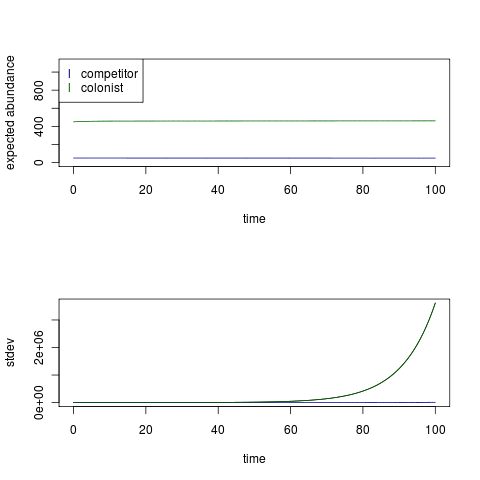
Image:Diverge.png
Image:Diverge.png

As this simulation clearly shows, even though I’ve started the population at the expected abundances and the average dynamics are stable, the variance term for the colonist diverges. With weaker c_2 it is easy to have equilibrium variances and have the expected variance of the competitor be larger than that of the colonist (despite smaller abundance).