Notes

Scratch notes on uncertainty.

Function definition: multiple_uncertainty.m

Settings:

f=@(x, h) max( (x-h) * (1 - (x-h) ./ 100) + (x-h), 0);
x_grid = [0:5:100];
h_grid = x_grid; % Must be same dimensions as x_grid, or L91 errors...  
Tmax = 5;
sigma_g = 0.1;
sigma_m = 0.;
sigma_i = 0.0;
delta = 0.05;
pdf = @(p,mu,s) lognpdf(p ./ mu, 0, s);
%pdf = @(p,mu,s) unifpdf(p, mu .* (1 - s), mu .* (1 + s)); 

[D, V, M, I, P, Ep, F, f_matrix] =  multiple_uncertainty(f, x_grid, h_grid, Tmax, sigma_g, sigma_m, sigma_i, delta, pdf);

Log normal noise gives the anticipated Reed solution:

Same settings but with uniform noise has a step:

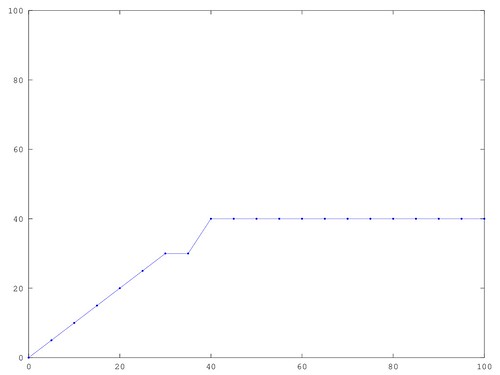
This step goes away under any one of the following tweaks:

• We use log-normal noise

Avoids the finite support problem that makes uniform noise look deterministic.

• We use delta = 0

Results in exact ties, but future isn’t discounted, so we choose the smallest h (default behavior of min() function for ties).

• Increase the noise size: sigma_g = 0.5 doesn’t remove the step. Smaller, non-zero noise sigma_g = 0.01, or sigma_g = 0.05 results in solutions with no escapement (under uniform noise; not a problem for log-normal noise).

• We use a finer mesh, which breaks this 1 step into lots of little steps.

Deterministic system (obviously independent of noise structure, since pdf isn’t used) has losts steps when delta \(> 0\).

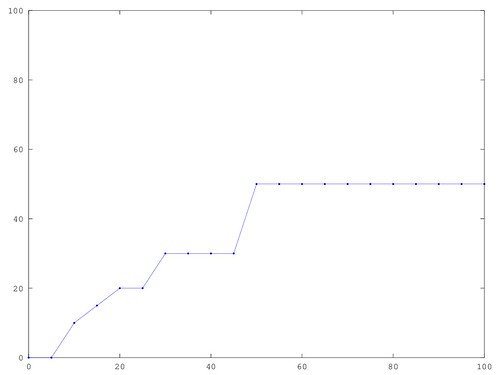
This is resolved by using the interpolation method to find the values off-grid.