(POWELL et. al. 2000)
Regimes
endemic - attack the weakling trees. epidemic
Tree has defenses. Aggregation of beetles can exhaust these, but then must disperse to other trees to avoid larval competition.
Mathematical Elements
The cast, (after some non-dimensionalization)
$ Q(x,y,t) = R P - Q R$ Nesting beetles
$ H(x,y,t) = R P - H R $ Holes: measures attack success
$ R(x,y,t) = ( 1 - R ) R - R H $ Resin: tree defense success
$ A(x,y,t) $ Some complex phermone plume, dependent on $ Q $
$ P(x,y,t) = -(vf(A)) - P)- P - RP + (x,y,t) $ Flying beetles diffuse
Density-based PDE
Hosting/nesting behavior: function of insect-pheromone response, host-tree vigor.
All about the competing processes $ Q $ and $ H $.
Local projection onto ODE system
Spatial dynamics play out in things that move ($ P $ and \(A \) ). Consider a focal tree of fixed density, and we can examine it’s impact on it’s radial neighbors by replacing the plume $ A $ with a function of nesting beetle number $ q \(, such that \) P $ can be described as infestation function on the current rate $ I(q) $.
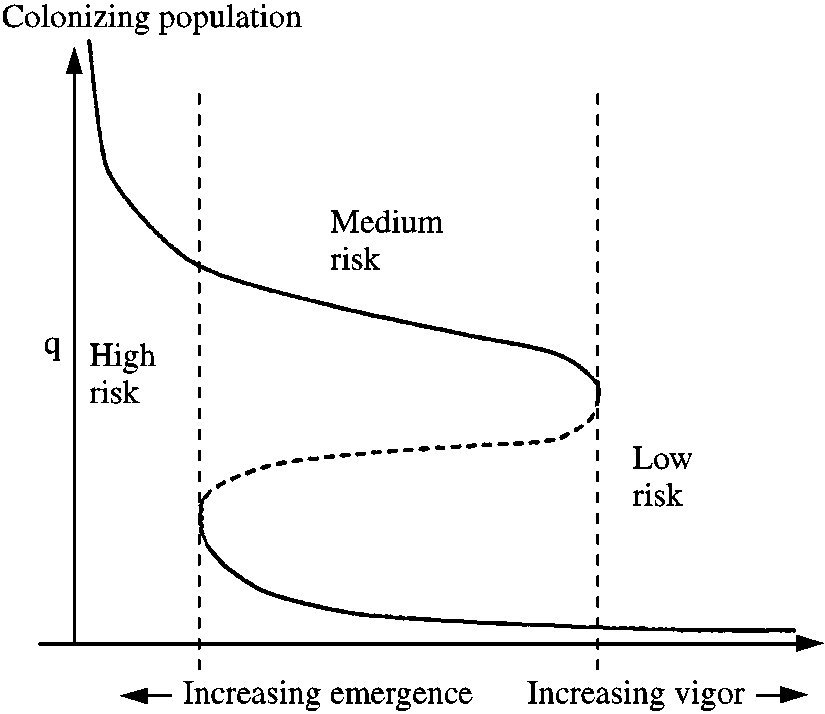
Stem-competition model
Becoming spatial again: with stand-growth model.
Factors:
stand age (changes tree vigor), older stands more robust due to thinning as well as individual robustness. But effect is weak since it can saturate quickly, old enough trees are safe.
emergence density (increases risk)
canopy closure (extends risk)
wind (disperses plume)
References
- POWELL J, KENNEDY B, WHITE P, BENTZ B, LOGAN J and ROBERTS D (2000). “Mathematical Elements of Attack Risk Analysis For Mountain Pine Beetles.” Journal of Theoretical Biology, 204. ISSN 00225193, https://dx.doi.org/10.1006/jtbi.2000.1080.