Consider a harvested fish population with discrete-time population dynamics under an allee effect:
\[ N_{t+1} = N_t \exp \left( \gamma \left[ 1-\frac{N_t}{K} \right] \left[ \frac{N_t - C}{K} \right] \right) - \beta E_h N_t\]
Note that C is the unfished allee threshold, K the carrying capacity, \(E_h\) the fish harvesting effort.
Consider that the initial population is unknown, but described by a density function whose variance can be decreased by sampling. Just to get started, let’s assume log-normal (avoiding the chance of negative population sizes), with log-standard deviation inversely proportional to the sampling effort $E_s $. For the moment we will only imagine sampling in the first year, then add the impact of sampling at later times eventually.
Write down the cost function as the sum of sampled cost of effort $ E_s $ and the expected profit over the uncertainty in the fish distribution.
…
see code (click-through figure for link to code).
hmm… optimum seems to drive fish to extinction. Poor choice of parameter value or something worse?
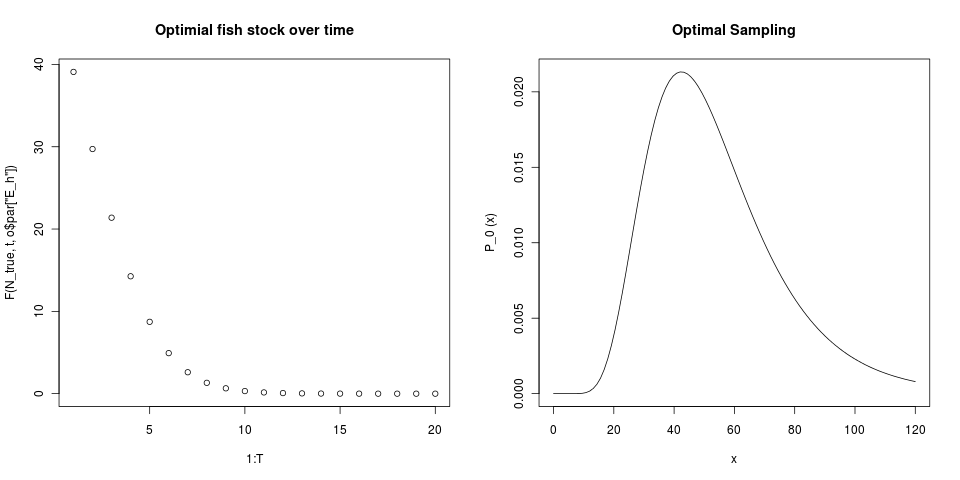
Should allow $ E_h $ to vary.