Runs from yesterday:
MLE comparison of full labrid pharyngeal innovation (all parrotfish), alpha-v-sigma: 

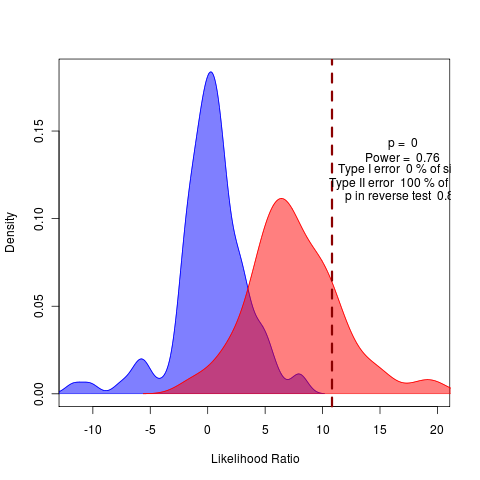
Unfortunately, the all-variable mcmc over labrid tree was unsuccessful.
Pure-brownie vs pure diversification ends up with the surprisingly opposite conclusion from the sigmas-alphas on parrotfish close ratio:
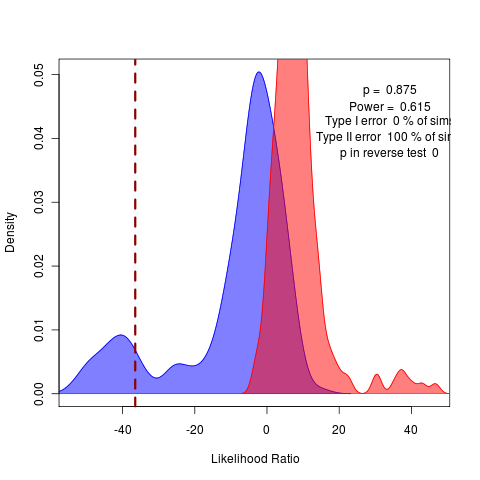
Clearly a convergence problem but with which model? (see parameter distributions adjacent; following in photostream archive).
Luckily this is not the case in the full labrid (size-corrected, protrusion, pharyngeal innovation) model set:
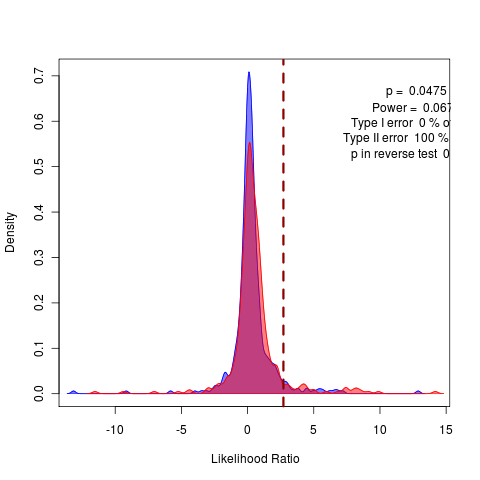
sigma model with alpha fixed at 1e-12, vs variable sigma, free, global alpha: 

Likelihoods well-behaved, indicating the importance of more data to navigate this ridge. letting alpha vary improves the fit, but not over the two-alphas model.
Unfortunately it seems even on the full labrid tree, the protrusion trait doesn’t have large enough differences to discriminate between the 5 parameter models; a clear indication of lack of power for this ridge. (Might be nice to compare the 5 parameter to their four parameter kin above)
Launched today:
labrid tree mcmc on prot with just alpha variable. (eleven n10) (3:44p)
parrotfish prot.y simple: alpha v sigma (n1), alpha v brownie. (zero n10) (3:44p)