7:30-9:30 Review for Theoretical Ecology
Profiling wrightscape
Compile with profiling (-g -pg flags, in make profile). Run
valgrind --leak-check-full ./wrightscape.exeto remove memory links. Run
valgrind --tool=callgrind
kcachegrind callgrind.out.<###>For profiling information
Troubleshooting implementation of restricted-domain functions. Cannot be wright_tree since they have to know their likelihood method. Will need an indicator to their type. Some troubleshooting of the simulation method too: my pmc’s montecarlotest() is set up so that simulate() can return the data set directly that is passed to update() or return a list object with the dataset in $rep.1. Up and running now.
Troubleshoot ouch-style search parameters. DONE – simulation didn’t include a rep command to copy a single alpha and sigma to be same in each regime.
Check convergence: sometimes the brownie-style search regime outperforms the wright-style (only 16 reps for testing purposes). Add convergence score to getParameters. DONE
Should be reported by C function version as well)
Convergence checks should be added to plot/summary functions from montecarlotest() output
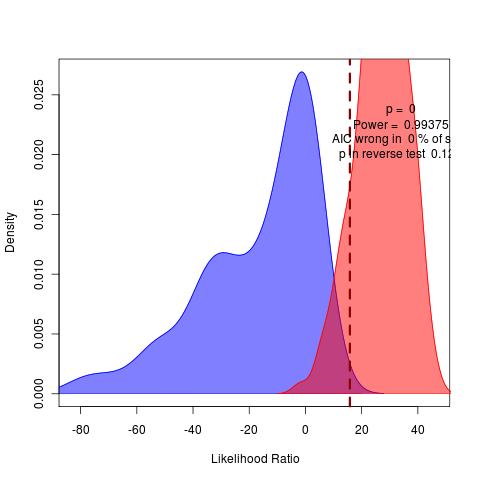
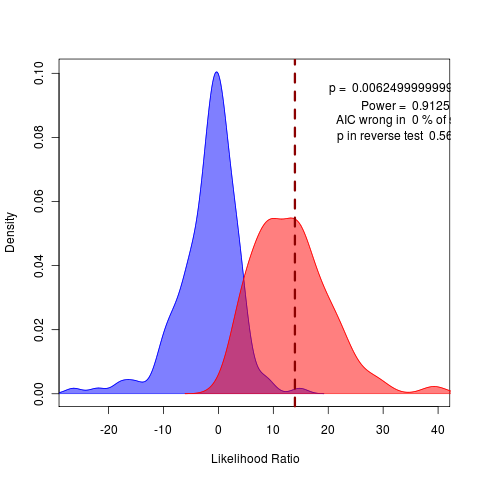
Running 160 reps of (my) brownie() vs wright() (on left) and also of brownie() vs wrightscape() (on right) at nice 10 on zero.
Data processing
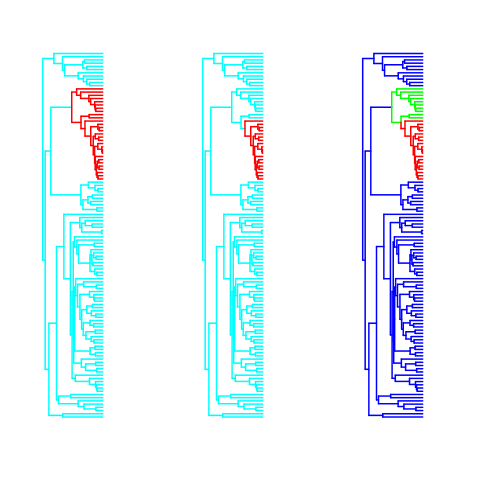
Need regimes for intramandibular joint: Chlorurus, Hipposcarus common ancestor. Easily done with maticce package:
intramandibular <- paintBranches(mrcaOUCH(c("Chlorurus_sordidus", "Hipposcarus_longiceps"), labrid$tree), labrid$tree, c("other","intramandibular"))Note that we need to look up and match species names exactly, otherwise instead of an error maticce assumes one of the species just isn’t in our tree and simply returns the root node.
Implemented each as a two regime model and combined as a three-regime model. combining requires arbitrarily assigning the branch between them so that it doesn’t become a separate node.
Convergence Issues
Clear examples of convergence issues on Nelder Mead stemming from initial conditions. For instance: even hansen routine can’t get the best optimum for two shifts (three regimes) when given the same starting points as it was for two regimes:
> ou2_intra <- hansen(trait, labrid$tree, regime=intramandibular, .01, .01)
> ou3 <- hansen(trait, labrid$tree, regime=two_shifts, .01, .01 )
> loglik(ou3) - loglik(ou2_phar)
[1] -2.473179Actually does worse than the model nested within it. Changing the starting conditions (using those from the nested model), it manages to find a better optimum.
> ou3 <- hansen(trait, labrid$tree, regime=two_shifts, [email protected], sigma=ou2_phar@sigma )
> loglik(ou3) - loglik(ou2_phar)
[1] 1.079799Convergence is certainly a larger issue with more parameters. One way to address this is focusing on comparing subcases of the general form. A particularly interesting one is the Release of Constraint: global theta and sigma, regime-specific alpha. IMPLEMENTED
Overall, best addressed by algorithmic methods for dealing with multiple peaks in the likelihood surface, such as simulated annealing or probably better, an EM algorithm ((Looking for packages to do this well, though may need a specific implementation. Will discuss in our Algorithms group in a few weeks Potentially take a closer look at this tutorial and em() in mclust package.)). Given the computational effort of these approaches, probably worth starting on the fully Bayesian implementation too.
Meanwhile, based on likelihoods alone, results seem promising, though needs some fiddling to test for convergence. For instance:
> loglik(release_twoshifts)
[1] 69.42358
> loglik(release_intra)
[1] 66.88511
> loglik(release_phar)
[1] 31.42613
> loglik(wright_twoshifts)
[1] 67.65605
> loglik(wright_intra)
[1] 70.40246See code for full example.