Numerical challenges in likelihood estimation of time-dep OU models

Worried about accurate maximum likelihood estimates of parameters, as the optimization could still converge on values not far from the starting conditions (not as surprising as the starting parameters are estimated intelligently first from the summary statistics) but could also vary depending on initial conditions.

Second, while it requires some re-parameterization, the stationary model for both linearized transcritical (LTC) bifurcation model and the linearized saddle-node (LSN) model are identically Ornstein-Uhlenbeck models. As this model is stationary, it’s unnecessary to continue numerically integrating the SDE to get the moments of the probability distribution, I can just use the analytic solution for the moments. I’ve written this in as a model class “constOU” in the likelihood_bifur_models.R library, which is of course much faster:

constOU <- function(Xo, to, t1, pars){
    Dt <- t1 - to
    Ex <- Xo*(1 - exp(-pars["Ro"]*Dt)) + pars["theta"]*exp(-pars["Ro"]*Dt) 
    Vx <- 0.5*pars["sigma"]^2 *(1-exp(-2*pars["Ro"]*Dt))/pars["Ro"]
    if(pars['Ro'] < 0 ) Vx = Inf 
    if(pars['sigma'] < 0 ) Vx = Inf 
    return(list(Ex=Ex, Vx=Vx))
}

Turning these parameters into those used by LTC should not require any scaling, while the estimated Ro becomes root Ro in LSN.

As I explored earlier, with linear change in stability the analytic expression for the moments gives some integrals that can be solved, but still leaves some to be done numerically, so integrating the moment equations directly seems just as well. Note that I’m still using the Gaussian character of the model to integrate the moments, by using the linear noise approximation:

## LSN
    moments <- function(t,y,p){ 
        sqrtR <- sqrt(R(t,pars)) 
        yd1 <- 2*sqrtR*(sqrtR+pars['theta'] - y[1]) 
        yd2 <- -2*sqrtR*y[2] + p["sigma"]^2*(sqrtR+pars['theta'])
        list(c(yd1=yd1, yd2=yd2))
    }
## LTC
    moments <- function(t,y,p){ 
        yd1 <- R(t,pars)*(pars['theta'] - y[1]) 
        yd2 <- -2*R(t,pars)*y[2] + p["sigma"]^2 ##check?
        list(c(yd1=yd1, yd2=yd2))
    }

Improving speed?

Attempting to improve the speed of the time-dependent fits. Most of the time is used by lsoda, not surprisingly. Worried that this time was simply in the initialization/allocation/cleanup of the integrator, which has to be called for each timestep in every calculation of the likelihood. If true, moving this into C I could have only a single allocation of the ode integrator which I could use for all timesteps, and I’d get a substantial speed increase.

R’s profile of time spent in lsoda:

$by.total
                          total.time total.pct self.time self.pct
"setmodel"                    322.26      99.7      0.00      0.0
"lapply"                      322.06      99.6      0.62      0.2
"<anonymous>"                 321.96      99.6    122.98     38.0
"setLTC"                      321.60      99.4      0.04      0.0
"FUN"                         321.38      99.4      2.34      0.7
"lik.gauss"                   320.02      99.0      0.02      0.0
"dc.gauss"                    319.78      98.9      0.00      0.0
"fn"                          319.38      98.8      0.00      0.0
"optim"                       319.38      98.8      0.00      0.0
"updateGauss"                 319.38      98.8      0.00      0.0
"lsoda"                       318.88      98.6     15.56      4.8
".Call"                       286.84      88.7     17.42      5.4

Not so much. Whole day of coding, debugging a few typos, and still bad performance when given long time intervals for the ode. Not clear why this is happening. See code here, may simply pull from future package.

Estimating Ro and the initial step-size for Nelder-Meade seem to be related to the issue – shrinking the step-size reduces the optimizer stalling, as does removing the dependence on “m” (the time-dependence) in the integration.

No go

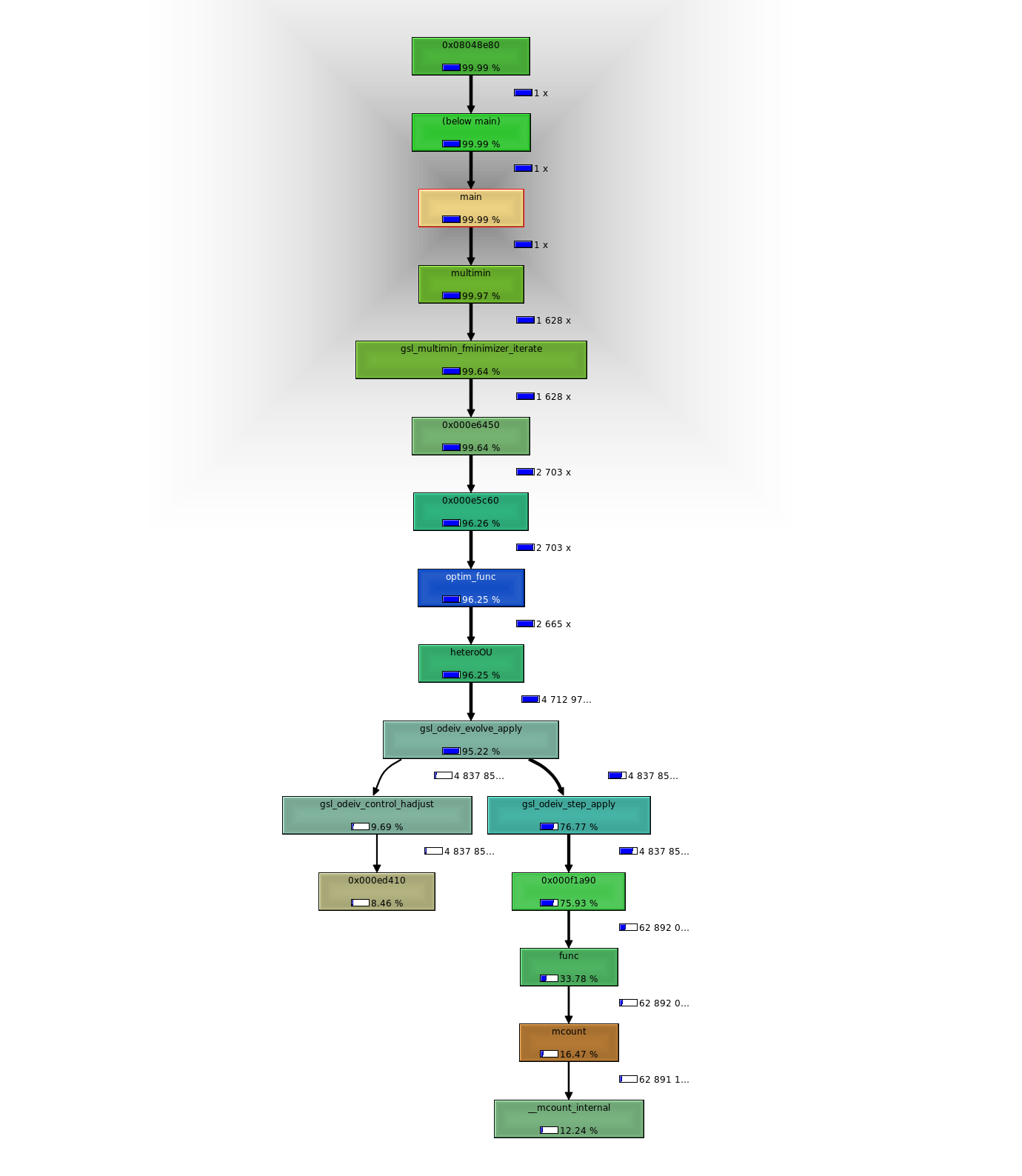
Whether the time is really being lost in the allocation also isn’t clear. We can compare this at least in the context of the C code: 5399 runs code initializing only once per likelihood calc (over 50 pts). Most time is spent applying the ode evolver. 5556 runs the code initializing every interval. So overall doesn’t seem like this approach can save as much time as I had hoped. Pity I couldn’t get profile results from R’s lsoda alloc first. Lot of programming just to perform these profiles.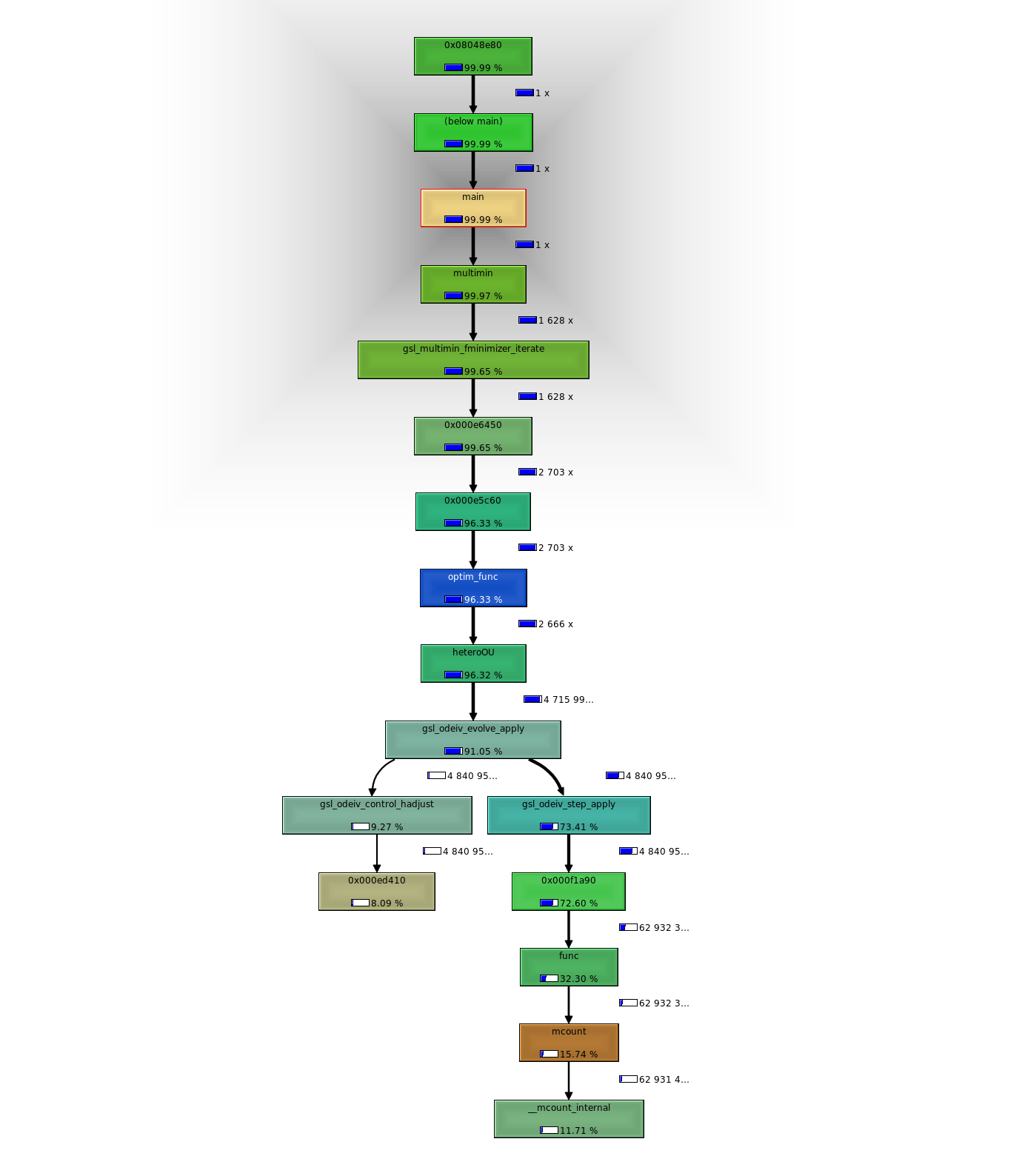

Better optimized searching

Several decent approximation routines to the likelihood of a generic (i.e. including our time-heterogeneous coefficients) SDE in Iacus’s sde package for R. Should probably pursue these instead, and continue the R based implementation. Need further study on convergence of estimates, but hopefully with faster likelihood optimization first. Will require a bit more exploring. Meanwhile, need more time on writing.