The variance dynamics are slightly different if the continuous time Markov process allows events to contain two steps (such as a transition of an individual from one age class to another, or one patch to another, etc) as well as one step birth/death) transitions. Vτ~*i**j~(X* / V) to represent the rate of transitions from state i to state j. We change variables for our state space from the discrete count state variable X by dividing by the system size (volume) V, to obtain the continuous, mean-field approximation of the density p = X/V. Then:

where T is a symmetric matrix with off-diagonal elements i,j τ~ij~(p) + τji(p) and diagonal elements chosen so that rows sum to zero. This approximation is implemented in noise_approx.R
Example: Crowley model
- Carl Boettiger 15:05, 25 May 2010 (EDT): (some corrections to eqns)
(Note this is the original Crowley model where the c coefficients are equal. In the original model this represented competition for space by overgrowth and hence would more naturally be expressed as a two step process).
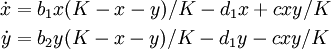
Interpreting the cxy terms as transitions rather than independent birth and death events results in the same mean-field dynamics but differing fluctuations. For instance, the covariance dynamics are:
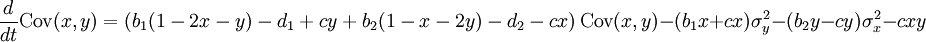
Whereas interpreted as single-step birth and death the cxy term at the end is absent.
The variance dynamics are similarly altered.
Numerical implementation
This individual-based simulation is implemented in metapop.c and callable from R interface from ind_based_models.R as metapop_ibm(). The file metapop.R specifies the dynamics of birth, death, transition matrix and the Jacobian so that linear_noise_approx() function from above can be used to calculate the moments. This file also runs the crolwey_ibm model (from crowley.c, interface in the ind_based.models.R) and the linear noise approximation to it from crowley.R to compare how the two-step process changes the noise dynamics.
This comparison can be run simply by loading the package and running metapop_example() function.
For some reason the individual based-simulation of the two-step process seems to resemble that of the one-step process more, while the two-step linear noise approximation alternately underestimates (Fig 1) or overestimates (Fig 2) the variance. Looking for bugs in the implementation at the moment.
- Carl Boettiger 21:43, 26 May 2010 (EDT): Bug found, see corrected graphs on Tuesday’s (5/25) entry.


Fig 1. Parameters: b_1 = .2, b_2 = .1, d_1 = d_2 = c = .1
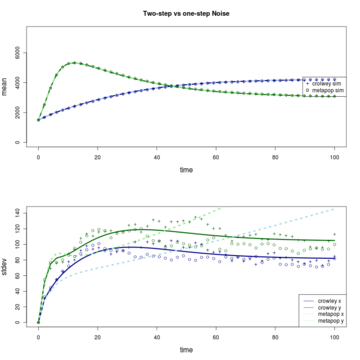

Fig. 2. Parameters: b_1 = .2, b_2 = .1, d_1 = d_2 = .1, c = .15